Что такое DDC SDR, комплексные сигналы и квадратурная обработка
| Повышение квалификации |
DDC - Digital Down Conversion (цифровое преобразование "вниз") - метод цифровой обработки сигналов, сочетающий квадратурное преобразование спектра исходного сигнала на нулевую промежуточную частоту, ограничение полосы и децимацию.
Оглавление
О комплексных сигналах и квадратурной обработке
О спектральных преобразованиях вещественных и комплексных сигналов
О зеркальном канале в традиционном SDR и DDC SDR
Принцип работы SDR приемника с DDC дециматором
Можно ли DDC реализовать при помощи вычислительно эффективной процедуры Быстрого Преобразования Фурье - FFT
О разрядности АЦП
О работе приемника DDC и передатчика DUC в высших зонах Найквиста
Зачем нужна рандомизация выходного кода АЦП в приемнике DDC-SDR
Нужна ли дизеризация в DDC-SDR приемнике
Об инверсии спектра дискретного (цифрового) сигнала
Литература
Сергиенко. Теоретические основы радиотехники
Сергиенко. Цифровая обработка сигналов
Гольденберг. Цифровая обработка сигналов
73! de UA4NE
О комплексных сигналах и квадратурной обработке
В природе существуют только сигналы вещественные - как функции времени s(t), в форме изменения во времени некоторой физической величины s. Комплексные же сигналы существуют только на бумаге в виде математических моделей или в нашем воображении. Наряду с теоретическими построениями, комплексные сигналы широко используются и в реальных технических устройствах, где раздельно обрабатываются в виде пары синхронных и взаимосвязанных (взаимно ортогональных, сопряженных по-Гильберту) вещественных сигналов - действительной части (Re, I, In-phase - синфазный канал) и мнимой части (Im, Q, Quadrature - квадратурный канал) комплексного сигнала. Такая обработка называется квадратурной. Ее основные достоинства - отсутствие побочных продуктов при спектральных преобразованиях, простота выполнения модуляции и демодуляции, т.е. помещения в сигнал и извлечения из сигнала информационных компонент.
В аналоговую эру радиолюбители обходили комплексные сигналы стороной, предпочитая бороться с зеркальными каналами в своих трансиверах при помощи многократного преобразования частоты. Причина этого в том, что пользу от квадратурной обработки можно получить лишь при достаточно точном выполнении операций, что при аналоговой реализации приводит к непропорционально большим издержкам. В конце прошлого века тему квадратурной обработки в трансиверах прямого преобразования активно продвигал В.Т. Поляков, где она применялась для подавления зеркального канала и формирования однополосного сигнала. Но только с появлением SDR, где большая часть обработки сигнала стала выполняться в цифровом виде, комплексные сигналы по-настоящему вошли в любительскую технику.
Математически один и тот же комплексный сигнал S(t) может быть записан в двух взаимосвязанных формах - в виде суммы действительной (Re) и мнимой (Im) частей, а также в показательной форме в виде комплексной экспоненты с модулем A и аргументом Ф:
S(t) = Re + i Im = A exp ( i Ф ),
A = SQRT ( Re * Re + Im * Im ),
Ф = arctg ( Im / Re ) + С.
Здесь i = SQRT (-1) - мнимая единица, SQRT - операция извлечения квадратного корня, С - константа 0 или пи, зависящая от знаков Re и Im, а величины Re, Im, A, Ф суть функции времени.
Эти соотношения позволяют в любой момент времени непрерывно и точно извлекать из принятого вещественного сигнала информационные компоненты: огибающую A и полную фазу Ф (по модулю 2 пи), если известны действительная и мнимая части комплексного сигнала. То есть, выполнять демодуляцию.
Обратные соотношения: Re = A Cos Ф, Im = A Sin Ф позволяют выполнять модуляцию.
Простой способ получить комплексный сигнал из исходного вещественного радиосигнала с ограниченным спектром и несущей Wo - умножить его на комплексную экспоненту exp ( -i Wo t ) = cos Wo t - i sin Wo t и при помощи фильтра выделить полезный продукт преобразования в окрестности нулевой частоты - комплексную огибающую (complex envelope). Такой комплексный сигнал удобен тем, что он не содержит несущей частоты Wo. Информационные компоненты А и Ф при демодуляции вычисляются из него напрямую, т.к. несущая не мешается под ногами. И наоборот, действительная и мнимая части комплексной огибающей при модуляции напрямую вычисляются из информационных компонент A и Ф.
Есть и другой способ, часто применяемый для сигналов, спектр которых ограничен только сверху (видеосигнал). Для того, чтобы получить из вещественного сигнала сопряженную с ним мнимую часть без преобразования частоты, применяют преобразователь (фильтр) Гильберта, который задерживает фазы всех спектральных составляющих сигнала на 90 градусов без искажения их амплитуд. Такой комплексный сигнал называется аналитическим сигналом. Его особенность в том, что спектр не содержит отрицательных частот, а несущая нескомпенсирована. Недостатки - физически реализуемый фильтр Гильберта блокирует постоянную составляющую и примыкающие к ней нижние частоты, а его выходной сигнал имеет задержку во времени на половину ширины апертуры фильтра (ширины скользящего окна обработки, интервала интегрирования, порядка нерекурсивного дискретного фильтра). Чем шире полоса сигнала и выше требования к качеству АЧХ/ФЧХ фильтра, тем эта задержка будет больше. Идеальный фильтр Гильберта физически нереализуем, его апертура и задержка были бы бесконечными. Для радиосигнала с бесконечно узким спектром фильтр Гильберта вырождается в простую линию задержки на пи-пополам.
Из аналитического сигнала можно получить комплексную огибающую (и наоборот) путем сдвига спектра в соответствующую сторону, т.е. простым умножением на комплексную экспоненту. Вещественный сигнал восстанавливается из аналитического простым отбрасыванием мнимой части. Примеры спектров обеих разновидностей комплексных сигналов можно посмотреть в следующем сообщении по теме о преобразовании спектров. Схема 3 в случае сдвига спектра вправо выполняет преобразование комплексной огибающей к аналитическому сигналу. Там же на схеме 4 дан пример восстановления вещественного сигнала из комплексной огибающей через промежуточное (но неполное) преобразование его к аналитическому сигналу.
Модуль спектра комплексного сигнала (в отличие от вещественного) не является четной функцией, то есть его спектр не симметричен относительно нулевой частоты. В комплексном сигнале можно отличить положительные частоты от отрицательных. Если мнимая часть какой-либо спектральной составляющей отстает по времени от действительной части - то эта частота положительная. А если опережает - то отрицательная. Конечно, опережение и отставание всегда должны быть строго на 90 градусов, так как действительная и мнимая части взаимно ортогональны (сопряжены по-Гильберту). Это означает, что на каждой частоте они соотносятся между собой как косинус и синус (косинус и минус синус). Нулевая частота в спектре комплексного сигнала ничем не выделяется и является равноправной со всеми остальными частотами.
Комплексные сигналы удобно наглядно представлять на комплексной плоскости, где по оси абсцисс откладывается действительная часть, а по оси ординат - мнимая, см. рисунок.
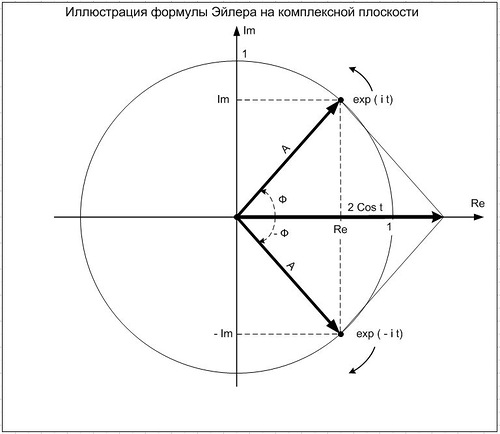
Комплексный сигнал положительной частоты exp ( i t ) = cos t + i sin t будет на этой комплексной плоскости представлен в виде точки, вращающейся с течением времени по окружности единичного радиуса против часовой стрелки со скоростью 1 оборот за 2 пи секунд. А сигнал отрицательной частоты exp ( -i t ) = cos t - i sin t будет вращаться так же, но по часовой стрелке. В каждый момент времени эти две точки будут симметричны относительно оси абсцисс. Такие два сигнала называются комплексно сопряженными, а их векторная сумма всегда будет вещественной косинусоидой, что показывает формула Эйлера: 2 cos t = exp ( i t ) + exp ( -i t ). Эта формула также показывает, что спектр вещественного косинуса симметричен относительно нулевой частоты и состоит из двух половинок: одна на положительной, а другая - на отрицательной частоте. Такой спектр называется двусторонним. Комплексный сигнал нулевой частоты exp ( i 0 t ) = cos 0 = 1 отображается на комплексной плоскости неподвижной точкой с координатами 1 + i 0. На комплексной плоскости хорошо видны взаимосвязи между величинами Re, Im, A, Ф, а вышеприведенные формулы для их взаимных преобразований следуют из элементарных геометрических построений.
Конечно, сами понятия положительной и отрицательной частоты, а также двустороннего спектра существуют только теоретически, когда мы рассматриваем сигналы через призму комплексных математических моделей. Но они нам дают в руки мощный инструмент анализа, который позволяет обобщить множество частных случаев.
Подробнее о комплексных числах и их свойствах: http://dsplib.ru/content/complex/complex.html
О преобразовании Гильберта (Hilbert Transform): http://dsplib.ru/content/hilbert/hilbert.html
В природе существуют только сигналы вещественные - как функции времени s(t), в форме изменения во времени некоторой физической величины s. Комплексные же сигналы существуют только на бумаге в виде математических моделей или в нашем воображении. Наряду с теоретическими построениями, комплексные сигналы широко используются и в реальных технических устройствах, где раздельно обрабатываются в виде пары синхронных и взаимосвязанных (взаимно ортогональных, сопряженных по-Гильберту) вещественных сигналов - действительной части (Re, I, In-phase - синфазный канал) и мнимой части (Im, Q, Quadrature - квадратурный канал) комплексного сигнала. Такая обработка называется квадратурной. Ее основные достоинства - отсутствие побочных продуктов при спектральных преобразованиях, простота выполнения модуляции и демодуляции, т.е. помещения в сигнал и извлечения из сигнала информационных компонент.
В аналоговую эру радиолюбители обходили комплексные сигналы стороной, предпочитая бороться с зеркальными каналами в своих трансиверах при помощи многократного преобразования частоты. Причина этого в том, что пользу от квадратурной обработки можно получить лишь при достаточно точном выполнении операций, что при аналоговой реализации приводит к непропорционально большим издержкам. В конце прошлого века тему квадратурной обработки в трансиверах прямого преобразования активно продвигал В.Т. Поляков, где она применялась для подавления зеркального канала и формирования однополосного сигнала. Но только с появлением SDR, где большая часть обработки сигнала стала выполняться в цифровом виде, комплексные сигналы по-настоящему вошли в любительскую технику.
Математически один и тот же комплексный сигнал S(t) может быть записан в двух взаимосвязанных формах - в виде суммы действительной (Re) и мнимой (Im) частей, а также в показательной форме в виде комплексной экспоненты с модулем A и аргументом Ф:
S(t) = Re + i Im = A exp ( i Ф ),
A = SQRT ( Re * Re + Im * Im ),
Ф = arctg ( Im / Re ) + С.
Здесь i = SQRT (-1) - мнимая единица, SQRT - операция извлечения квадратного корня, С - константа 0 или пи, зависящая от знаков Re и Im, а величины Re, Im, A, Ф суть функции времени.
Эти соотношения позволяют в любой момент времени непрерывно и точно извлекать из принятого вещественного сигнала информационные компоненты: огибающую A и полную фазу Ф (по модулю 2 пи), если известны действительная и мнимая части комплексного сигнала. То есть, выполнять демодуляцию.
Обратные соотношения: Re = A Cos Ф, Im = A Sin Ф позволяют выполнять модуляцию.
Простой способ получить комплексный сигнал из исходного вещественного радиосигнала с ограниченным спектром и несущей Wo - умножить его на комплексную экспоненту exp ( -i Wo t ) = cos Wo t - i sin Wo t и при помощи фильтра выделить полезный продукт преобразования в окрестности нулевой частоты - комплексную огибающую (complex envelope). Такой комплексный сигнал удобен тем, что он не содержит несущей частоты Wo. Информационные компоненты А и Ф при демодуляции вычисляются из него напрямую, т.к. несущая не мешается под ногами. И наоборот, действительная и мнимая части комплексной огибающей при модуляции напрямую вычисляются из информационных компонент A и Ф.
Есть и другой способ, часто применяемый для сигналов, спектр которых ограничен только сверху (видеосигнал). Для того, чтобы получить из вещественного сигнала сопряженную с ним мнимую часть без преобразования частоты, применяют преобразователь (фильтр) Гильберта, который задерживает фазы всех спектральных составляющих сигнала на 90 градусов без искажения их амплитуд. Такой комплексный сигнал называется аналитическим сигналом. Его особенность в том, что спектр не содержит отрицательных частот, а несущая нескомпенсирована. Недостатки - физически реализуемый фильтр Гильберта блокирует постоянную составляющую и примыкающие к ней нижние частоты, а его выходной сигнал имеет задержку во времени на половину ширины апертуры фильтра (ширины скользящего окна обработки, интервала интегрирования, порядка нерекурсивного дискретного фильтра). Чем шире полоса сигнала и выше требования к качеству АЧХ/ФЧХ фильтра, тем эта задержка будет больше. Идеальный фильтр Гильберта физически нереализуем, его апертура и задержка были бы бесконечными. Для радиосигнала с бесконечно узким спектром фильтр Гильберта вырождается в простую линию задержки на пи-пополам.
Из аналитического сигнала можно получить комплексную огибающую (и наоборот) путем сдвига спектра в соответствующую сторону, т.е. простым умножением на комплексную экспоненту. Вещественный сигнал восстанавливается из аналитического простым отбрасыванием мнимой части. Примеры спектров обеих разновидностей комплексных сигналов можно посмотреть в следующем сообщении по теме о преобразовании спектров. Схема 3 в случае сдвига спектра вправо выполняет преобразование комплексной огибающей к аналитическому сигналу. Там же на схеме 4 дан пример восстановления вещественного сигнала из комплексной огибающей через промежуточное (но неполное) преобразование его к аналитическому сигналу.
Модуль спектра комплексного сигнала (в отличие от вещественного) не является четной функцией, то есть его спектр не симметричен относительно нулевой частоты. В комплексном сигнале можно отличить положительные частоты от отрицательных. Если мнимая часть какой-либо спектральной составляющей отстает по времени от действительной части - то эта частота положительная. А если опережает - то отрицательная. Конечно, опережение и отставание всегда должны быть строго на 90 градусов, так как действительная и мнимая части взаимно ортогональны (сопряжены по-Гильберту). Это означает, что на каждой частоте они соотносятся между собой как косинус и синус (косинус и минус синус). Нулевая частота в спектре комплексного сигнала ничем не выделяется и является равноправной со всеми остальными частотами.
Комплексные сигналы удобно наглядно представлять на комплексной плоскости, где по оси абсцисс откладывается действительная часть, а по оси ординат - мнимая, см. рисунок.

Комплексный сигнал положительной частоты exp ( i t ) = cos t + i sin t будет на этой комплексной плоскости представлен в виде точки, вращающейся с течением времени по окружности единичного радиуса против часовой стрелки со скоростью 1 оборот за 2 пи секунд. А сигнал отрицательной частоты exp ( -i t ) = cos t - i sin t будет вращаться так же, но по часовой стрелке. В каждый момент времени эти две точки будут симметричны относительно оси абсцисс. Такие два сигнала называются комплексно сопряженными, а их векторная сумма всегда будет вещественной косинусоидой, что показывает формула Эйлера: 2 cos t = exp ( i t ) + exp ( -i t ). Эта формула также показывает, что спектр вещественного косинуса симметричен относительно нулевой частоты и состоит из двух половинок: одна на положительной, а другая - на отрицательной частоте. Такой спектр называется двусторонним. Комплексный сигнал нулевой частоты exp ( i 0 t ) = cos 0 = 1 отображается на комплексной плоскости неподвижной точкой с координатами 1 + i 0. На комплексной плоскости хорошо видны взаимосвязи между величинами Re, Im, A, Ф, а вышеприведенные формулы для их взаимных преобразований следуют из элементарных геометрических построений.
Конечно, сами понятия положительной и отрицательной частоты, а также двустороннего спектра существуют только теоретически, когда мы рассматриваем сигналы через призму комплексных математических моделей. Но они нам дают в руки мощный инструмент анализа, который позволяет обобщить множество частных случаев.
Подробнее о комплексных числах и их свойствах: http://dsplib.ru/content/complex/complex.html
О преобразовании Гильберта (Hilbert Transform): http://dsplib.ru/content/hilbert/hilbert.html
О спектральных преобразованиях вещественных и комплексных сигналов
Для того, чтобы преобразовать (т.е. линейно сдвинуть по оси частот вправо или влево на величину Wo = 2 пи Fo рад/сек) симметричный спектр вещественного сигнала s(t), этот сигнал нужно умножить на комплексную экспоненту соответственно положительной или отрицательной частоты Wo:
s(t) exp ( i Wo t ) = s(t) cos (Wo t) + i s(t) sin (Wo t) - сдвиг вправо,
s(t) exp ( -i Wo t) = s(t) cos (Wo t) - i s(t) sin (Wo t) - сдвиг влево.
При этом на выходе преобразователя получается комплексный сигнал (Re + i Im) с несимметричным спектром. Эти случаи рассмотрены на верхнем рисунке во вложении, схемы 1 и 2 соответственно. Направление сдвига спектра определяется знаком плюс или минус при умножаемой опорной синусоиде (мнимой части комплексной экспоненты). Как правило, полезным является продукт преобразования, сосредоточенный вокруг нулевой частоты (комплексная огибающая, complex envelope). При этом "вторая половинка" спектра исходного сигнала образует продукт вокруг частот 2Wo или -2Wo, который часто нам мешает и удаляется при помощи ФНЧ.
Схема 2 применяется в классическом SDR, DDC, DFT и т. д.
Схема 1 применяется, если требуется инвертировать спектр комплексной огибающей.
Для того, чтобы так же преобразовать спектр комплексного сигнала, требуется сделать ровно то же самое, т.е. умножить этот сигнал на комплексную экспоненту положительной или отрицательной частоты Wo. Эти случаи рассмотрены на нижнем рисунке на схеме 3, при этом направление сдвига спектра также определяется знаками при умножаемых опорных синусоидах. Схема умножителя при этом усложняется, так как перемножаются уже два комплексных сигнала (оба сигнала содержат действительную Re и мнимую Im части, раскрываем скобки):
(Re1 + i Im1) (Re2 + i Im2) = (Re1 Re2 - Im1 Im2) + i (Re2 Im1 + Re1 Im2) - сдвиг вправо,
(Re1 + i Im1) (Re2 - i Im2) = (Re1 Re2 + Im1 Im2) + i (Re2 Im1 - Re1 Im2) - сдвиг влево.
Здесь требуется уже четыре умножителя и два сумматора. Инверсия знака при произведении Im1 Im2 получается из-за того, что квадрат мнимой единицы (i x i) = -1.
На схеме 4 показана операция восстановления вещественного сигнала из комплексного, например, чтобы его можно было послушать или передать в канал связи. При этом задействуется только та часть схемы 3, которая вычисляет действительную часть комплексного произведения. Мнимая часть не вычисляется, т.к. у вещественного сигнала она отсутствует. В результате отбрасывания мнимой части, спектр продукта преобразования становится симметричным, а сигнал - вещественным.
Все рассмотренные преобразования при условии их точного выполнения не приводят к появлению зеркальных каналов. Однако, опасность зеркального канала имеется в схеме 4 в случае, если перед отбрасыванием мнимой части спектр комплексного продукта (как бы вычисляемого по схеме 3) не будет состоять целиком из частот одинакового знака.
Если все наши сигналы являются дискретными (цифровыми), то функциональные схемы преобразователей остаются прежними. Однако при этом все спектры на картинках должны быть нарисованы периодическими в обе стороны по частоте. Период повторения спектра дискретного сигнала равен частоте дискретизации.
Для того, чтобы преобразовать (т.е. линейно сдвинуть по оси частот вправо или влево на величину Wo = 2 пи Fo рад/сек) симметричный спектр вещественного сигнала s(t), этот сигнал нужно умножить на комплексную экспоненту соответственно положительной или отрицательной частоты Wo:
s(t) exp ( i Wo t ) = s(t) cos (Wo t) + i s(t) sin (Wo t) - сдвиг вправо,
s(t) exp ( -i Wo t) = s(t) cos (Wo t) - i s(t) sin (Wo t) - сдвиг влево.
При этом на выходе преобразователя получается комплексный сигнал (Re + i Im) с несимметричным спектром. Эти случаи рассмотрены на верхнем рисунке во вложении, схемы 1 и 2 соответственно. Направление сдвига спектра определяется знаком плюс или минус при умножаемой опорной синусоиде (мнимой части комплексной экспоненты). Как правило, полезным является продукт преобразования, сосредоточенный вокруг нулевой частоты (комплексная огибающая, complex envelope). При этом "вторая половинка" спектра исходного сигнала образует продукт вокруг частот 2Wo или -2Wo, который часто нам мешает и удаляется при помощи ФНЧ.
Схема 2 применяется в классическом SDR, DDC, DFT и т. д.
Схема 1 применяется, если требуется инвертировать спектр комплексной огибающей.
Для того, чтобы так же преобразовать спектр комплексного сигнала, требуется сделать ровно то же самое, т.е. умножить этот сигнал на комплексную экспоненту положительной или отрицательной частоты Wo. Эти случаи рассмотрены на нижнем рисунке на схеме 3, при этом направление сдвига спектра также определяется знаками при умножаемых опорных синусоидах. Схема умножителя при этом усложняется, так как перемножаются уже два комплексных сигнала (оба сигнала содержат действительную Re и мнимую Im части, раскрываем скобки):
(Re1 + i Im1) (Re2 + i Im2) = (Re1 Re2 - Im1 Im2) + i (Re2 Im1 + Re1 Im2) - сдвиг вправо,
(Re1 + i Im1) (Re2 - i Im2) = (Re1 Re2 + Im1 Im2) + i (Re2 Im1 - Re1 Im2) - сдвиг влево.
Здесь требуется уже четыре умножителя и два сумматора. Инверсия знака при произведении Im1 Im2 получается из-за того, что квадрат мнимой единицы (i x i) = -1.
На схеме 4 показана операция восстановления вещественного сигнала из комплексного, например, чтобы его можно было послушать или передать в канал связи. При этом задействуется только та часть схемы 3, которая вычисляет действительную часть комплексного произведения. Мнимая часть не вычисляется, т.к. у вещественного сигнала она отсутствует. В результате отбрасывания мнимой части, спектр продукта преобразования становится симметричным, а сигнал - вещественным.
Все рассмотренные преобразования при условии их точного выполнения не приводят к появлению зеркальных каналов. Однако, опасность зеркального канала имеется в схеме 4 в случае, если перед отбрасыванием мнимой части спектр комплексного продукта (как бы вычисляемого по схеме 3) не будет состоять целиком из частот одинакового знака.
Если все наши сигналы являются дискретными (цифровыми), то функциональные схемы преобразователей остаются прежними. Однако при этом все спектры на картинках должны быть нарисованы периодическими в обе стороны по частоте. Период повторения спектра дискретного сигнала равен частоте дискретизации.
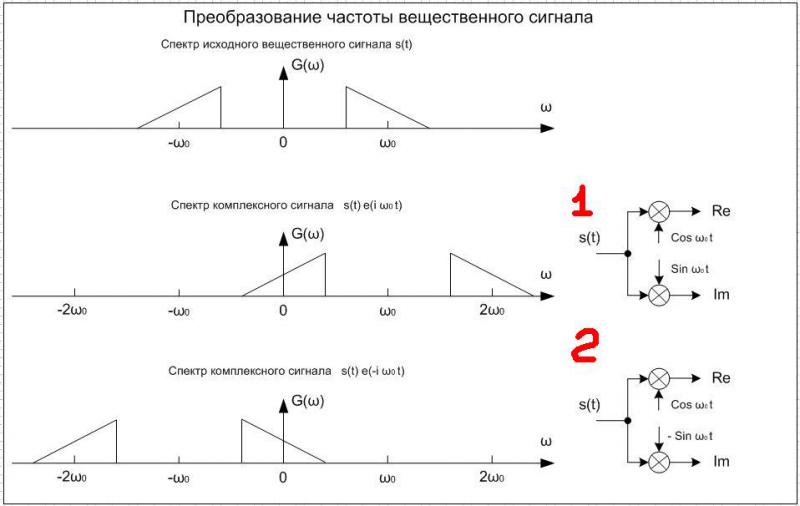
Спектральные преобразования вещественного сигнала
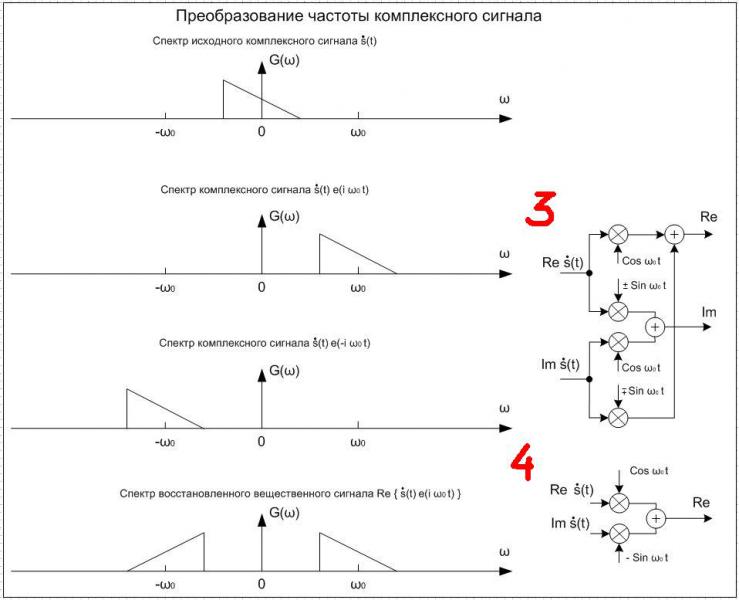
Спектральные преобразования комплексного сигнала
О зеркальном канале в традиционном SDR и DDC SDR
Откуда берется зеркальный канал в обычном (неквадратурном) преобразователе частоты обычного супергетеродина - это знают все. Причина проста - у вещественного сигнала спектр симметричен относительно нулевой частоты. И если мы смотрим на обычную вещественную косинусоиду, мы не можем сказать, какая у нее частота - положительная или отрицательная. Потому что у косинусоиды (равно как и у синусоиды) одновременно присутствуют обе эти компоненты, каждой по половинке. Эти компоненты комплексно-сопряжены, и их векторная сумма всегда дает вещественную (ко)синусоиду (см. формулу Эйлера). Так вот, эта "вторая половинка" и является источником зеркального канала.
Ситуация в корне меняется, если наш сигнал комплексный, а преобразователь частоты - квадратурный. На его выходе мы имеем комплексную огибающую (complex envelope) - это есть такая разновидность комплексного сигнала, у которого спектр сосредоточен по обе стороны вокруг нулевой частоты. Иногда говорят Zero IF, подчеркивая, что эта нулевая частота - промежуточная, а сам сигнал - комплексный. У такого комплексного сигнала всегда можно сказать, какая частота положительная, и какая - отрицательная. То есть, они суть разные. Спектр комплексного сигнала никогда не бывает симметричным относительно нулевой частоты и никаких "вторых половинок" в нём нет. И именно поэтому любые спектральные преобразования с комплексными сигналами никаких побочных продуктов не дают. В том числе не дают и зеркальных каналов. Это одна из причин широкого применения квадратурной обработки в технике. Но она должна выполняться как можно более точно.
В SDR приемниках применяется квадратурное преобразование частоты, это значит, что теоретически зеркального канала в них быть не должно. Но почему же в традиционном SDR (см. рис.) всё-таки присутствует зеркальный канал, несмотря на комплексный выходной сигнал квадратурного преобразователя?
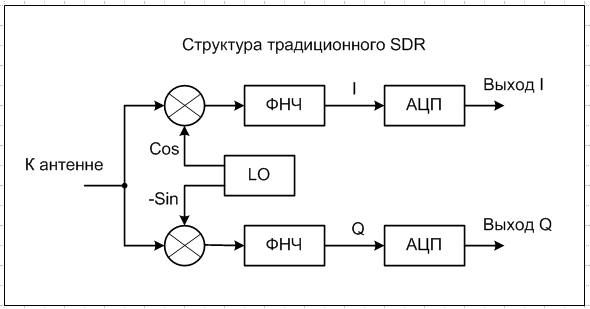
Причина тоже проста - этот преобразователь выполнен в аналоговом виде, а значит, он не идеален и в принципе идеальным быть не может. Как и всё аналоговое в нашем мире. Перечислю факторы, которые влияют на уровень зеркалки в традиционном SDR:
- неидентичность амплитуд синуса и косинуса у генератора LO;
- отличие разности фаз синуса и косинуса у генератора LO от требуемых 90 градусов;
- неидентичность аналоговых перемножителей между собой;
- неидентичность АЧХ и ФЧХ аналоговых фильтров в цепях синфазного и квадратурного каналов преобразователя;
- неидентичность каналов звуковой карты.
При этом можно ориентироваться на такие оценочные цифры. Разница амплитуд в синфазном и квадратурном каналах 1% дает примерно минус 45 dBc зеркалки, а расфазировка в 1 градус между этими каналами дает примерно -40 dBc (см. на рисунке результат совместного влияния этих погрешностей). Типовые погрешности современных аналоговых квадратурных преобразователей пляшут около этих цифр. У комплексных сигналов зеркальный канал расположен симметрично основному каналу относительно нулевой частоты - это неполностью подавленный остаток от "второй половинки" спектра вещественного сигнала.
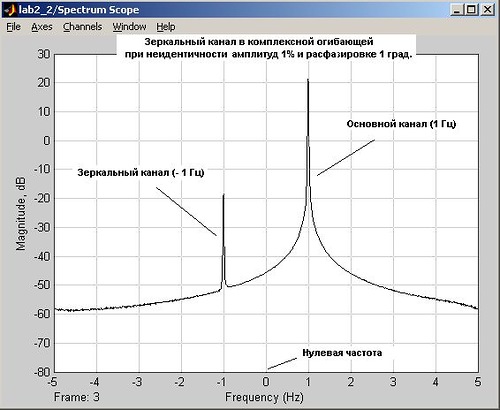
Если все эти неидентичности и неидеальности аналогового квадратурного преобразователя устранить, то и зеркалка исчезнет. Но увы, это невозможно сделать во всей рабочей полосе частот. А если бы нам это и удалось, например, при помощи предварительно выполненной калибровки, то всегда остается температурная нестабильность и старение аналоговых элементов фильтра. Конечно, существуют адаптивные алгоритмы цифрового подавления зеркалки "на лету", основанные на анализе квадратур после АЦП в реальном времени, но это не панацея - максимум что они могут (да и то для ограниченного класса сигналов) - это додавить зеркалку до минус 70-80 dBc, при этом внося в сигнал дополнительные нелинейные искажения. К слову, приемная часть любого мобильного телефона, WI-FI точки доступа, GPS приемника и т.д. построена именно по такой структурной схеме - с аналоговым квадратурным преобразователем и последующей оцифровкой комплексной огибающей двухканальным АЦП. То есть, они суть традиционные SDR со всеми достоинствами и недостатками.
При цифровой же реализации квадратурного преобразователя в DDC SDR, построенном по принципу "АЦП к антенне", все операции обработки сигнала в нём выполняются в цифровом виде и выполняются точно (с учетом погрешности вычислений из-за ограниченной разрядности) и абсолютно идентично в обоих каналах I и Q. Синус и косинус в блоке DDS (direct digital synthesizer) также формируются достаточно точно. Поэтому в DDC SDR приемнике зеркальный канал подавлен более чем на 100 дБ, и его не видно под шумами. Зеркальный канал появится, если в такой преобразователь искуственно внести погрешность, например, изменить порядок фильтра в одном из каналов. Или внести любую другую погрешность в вычисления.
Но в DDC SDR есть другие причины побочных каналов приема. Они появляются как следствие неграмотного проектирования дециматора и в принципе устранимы.
Откуда берется зеркальный канал в обычном (неквадратурном) преобразователе частоты обычного супергетеродина - это знают все. Причина проста - у вещественного сигнала спектр симметричен относительно нулевой частоты. И если мы смотрим на обычную вещественную косинусоиду, мы не можем сказать, какая у нее частота - положительная или отрицательная. Потому что у косинусоиды (равно как и у синусоиды) одновременно присутствуют обе эти компоненты, каждой по половинке. Эти компоненты комплексно-сопряжены, и их векторная сумма всегда дает вещественную (ко)синусоиду (см. формулу Эйлера). Так вот, эта "вторая половинка" и является источником зеркального канала.
Ситуация в корне меняется, если наш сигнал комплексный, а преобразователь частоты - квадратурный. На его выходе мы имеем комплексную огибающую (complex envelope) - это есть такая разновидность комплексного сигнала, у которого спектр сосредоточен по обе стороны вокруг нулевой частоты. Иногда говорят Zero IF, подчеркивая, что эта нулевая частота - промежуточная, а сам сигнал - комплексный. У такого комплексного сигнала всегда можно сказать, какая частота положительная, и какая - отрицательная. То есть, они суть разные. Спектр комплексного сигнала никогда не бывает симметричным относительно нулевой частоты и никаких "вторых половинок" в нём нет. И именно поэтому любые спектральные преобразования с комплексными сигналами никаких побочных продуктов не дают. В том числе не дают и зеркальных каналов. Это одна из причин широкого применения квадратурной обработки в технике. Но она должна выполняться как можно более точно.
В SDR приемниках применяется квадратурное преобразование частоты, это значит, что теоретически зеркального канала в них быть не должно. Но почему же в традиционном SDR (см. рис.) всё-таки присутствует зеркальный канал, несмотря на комплексный выходной сигнал квадратурного преобразователя?

Причина тоже проста - этот преобразователь выполнен в аналоговом виде, а значит, он не идеален и в принципе идеальным быть не может. Как и всё аналоговое в нашем мире. Перечислю факторы, которые влияют на уровень зеркалки в традиционном SDR:
- неидентичность амплитуд синуса и косинуса у генератора LO;
- отличие разности фаз синуса и косинуса у генератора LO от требуемых 90 градусов;
- неидентичность аналоговых перемножителей между собой;
- неидентичность АЧХ и ФЧХ аналоговых фильтров в цепях синфазного и квадратурного каналов преобразователя;
- неидентичность каналов звуковой карты.
При этом можно ориентироваться на такие оценочные цифры. Разница амплитуд в синфазном и квадратурном каналах 1% дает примерно минус 45 dBc зеркалки, а расфазировка в 1 градус между этими каналами дает примерно -40 dBc (см. на рисунке результат совместного влияния этих погрешностей). Типовые погрешности современных аналоговых квадратурных преобразователей пляшут около этих цифр. У комплексных сигналов зеркальный канал расположен симметрично основному каналу относительно нулевой частоты - это неполностью подавленный остаток от "второй половинки" спектра вещественного сигнала.

Если все эти неидентичности и неидеальности аналогового квадратурного преобразователя устранить, то и зеркалка исчезнет. Но увы, это невозможно сделать во всей рабочей полосе частот. А если бы нам это и удалось, например, при помощи предварительно выполненной калибровки, то всегда остается температурная нестабильность и старение аналоговых элементов фильтра. Конечно, существуют адаптивные алгоритмы цифрового подавления зеркалки "на лету", основанные на анализе квадратур после АЦП в реальном времени, но это не панацея - максимум что они могут (да и то для ограниченного класса сигналов) - это додавить зеркалку до минус 70-80 dBc, при этом внося в сигнал дополнительные нелинейные искажения. К слову, приемная часть любого мобильного телефона, WI-FI точки доступа, GPS приемника и т.д. построена именно по такой структурной схеме - с аналоговым квадратурным преобразователем и последующей оцифровкой комплексной огибающей двухканальным АЦП. То есть, они суть традиционные SDR со всеми достоинствами и недостатками.
При цифровой же реализации квадратурного преобразователя в DDC SDR, построенном по принципу "АЦП к антенне", все операции обработки сигнала в нём выполняются в цифровом виде и выполняются точно (с учетом погрешности вычислений из-за ограниченной разрядности) и абсолютно идентично в обоих каналах I и Q. Синус и косинус в блоке DDS (direct digital synthesizer) также формируются достаточно точно. Поэтому в DDC SDR приемнике зеркальный канал подавлен более чем на 100 дБ, и его не видно под шумами. Зеркальный канал появится, если в такой преобразователь искуственно внести погрешность, например, изменить порядок фильтра в одном из каналов. Или внести любую другую погрешность в вычисления.
Но в DDC SDR есть другие причины побочных каналов приема. Они появляются как следствие неграмотного проектирования дециматора и в принципе устранимы.
Принцип работы SDR приемника с DDC дециматором
Рассмотрим типовую структуру КВ цифрового приемника с DDC дециматором.
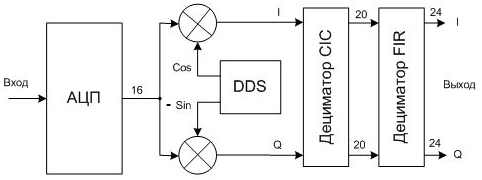
Для конкретности пусть частота дискретизации АЦП будет 100 МГц, а ширина целевой полосы выходного сигнала 2 МГц. Берем "с потолка" запас 0,5 МГц на неидеальность децимирующего фильтра, итого получаем частоту дискретизации комплексного выходного сигнала 2,5 МГц. Таким образом, в процессе обработки требуется понизить (децимировать) частоту дискретизации в 40 раз. Вся обработка принятого сигнала (после АЦП) выполняется вычислительными алгоритмами цифровой обработки сигналов (ЦОС), то есть, достаточно точно.
На выходе АЦП мы имеем вещественный дискретный сигнал с симметричным относительно нуля периодическим спектром (период 100 МГц). Квадратурный преобразователь (DDS и два умножителя) формирует из этого вещественного сигнала комплексный дискретный сигнал и линейно сдвигает его спектр по оси частот так, чтобы центральная частота целевой полосы стала нулевой промежуточной частотой. При этом периодичность спектра сохраняется, но он перестает быть симметричным (это и понятно, сигнал стал комплексным), см. рисунок.
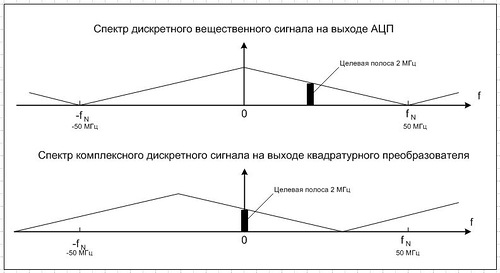
Цель дальнейшей фильтрации - из широкой 100-мегагерцовой полосы комплексного сигнала вырезать нужные нам 2 МГц в окрестности нулевой частоты с одновременным выполнением децимации. Эта операция выполняется параллельно в обоих I-Q каналах независимо друг от друга обычными дискретными (цифровыми) вещественными фильтрами. Фильтры должны быть абсолютно идентичными. Рекомендуется применять нерекурсивные фильтры с симметричными коэффициентами.
Операция децимации заключается в отбрасывании лишних отсчетов дискретного сигнала. Грубо говоря, на выходе из сорока пар исходных отсчетов сигнала должна остаться только одна пара. Так просто их отбросить нельзя, иначе будет эффект спектральных наложений (алайзинг), т.к. по сути децимация - это дискретизация дискретного сигнала. Т.е. перед отбрасыванием мы должны спектр сигнала привести к требованиям по-Котельникову, отфильтровать те частоты, которые превышают новую частоту Найквиста. От рекурсивных фильтров отказываемся, т.к. нам не нужна кривая ФЧХ. Значит, нерекурсивный FIR фильтр должен быть немалого порядка, с хорошим скатом АЧХ - ведь на расфильтровку у нас есть всего 500 кГц запаса.
Анализируя эту ситуацию, мы видим, что у нас нет такого огромного вычислительного ресурса - ведь оба децимирующих FIR фильтра должны работать на полной скорости 100 MSPS. Да и вообще - наша дешевая ПЛИС не имеет столько встроенных умножителей для их реализации. Что делать?
И тут нам на помощь приходит самая простейшая из всех простых форма реализации нерекурсивного фильтра - однородный фильтр. Это такой фильтр, все коэффициенты которого равны единице. То есть, он не требует умножителей совсем! Импульсная характеристика (взвешивающее окно) однородного фильтра - прямоугольная, а АЧХ (модуль преобразования Фурье импульсной характеристики) имеет многолепестковую форму, в которой лепестки образованы функцией вида |sinc x| = |sin x / x|. Затухание АЧХ в средних точках между лепестками бесконечное. Этот фильтр может быть реализован и в рекурсивном виде, так он получается еще проще. Теория однородного фильтра изложена у Гольденберга ("Цифровая обработка сигналов") на странице 77. Супостаты Гольденберга не читали, и рекурсивную реализацию однородного фильтра они по-своему обозвали CIC-фильтром (Cascaded Integral-Comb), или фильтром Хогенауэра.
К нашей радости оказывается, что его АЧХ как нельзя лучше подходит для реализации децимирующего фильтра, т.к. имеет глубокие провалы как раз на тех частотах, где требуется давить "алиасы". См. на рисунке АЧХ 1-каскадного CIC, рассчитанного для коэффициента децимации 10. Ось частот отградуирована в долях от исходной частоты дискретизации, т.е. 0,5 - это исходная частота Найквиста 50 МГц. Новая частота дискретизации после этого дециматора будет 100/10 = 10 МГц.
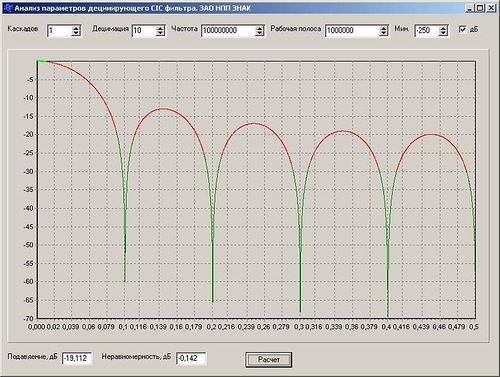
На картинке красным цветом показаны полосы частот, которые нас не интересуют вообще и где АЧХ может быть абсолютно любой (это и не целевая полоса и не алиасы), зеленым цветом близ нулевой частоты показана половина 2-мегагерцовой целевой полосы, также зеленым цветом вокруг провалов на частотах кратных новой частоте дискретизации 10 МГц (10, 20, 30, 40, 50 МГц) показаны 2-мегагерцовые участки "алиасов". К сожалению, эти провалы АЧХ не столь широки как нам хотелось бы, и на краях полезной полосы алиас первого порядка будет подавлен всего на 19 дБ. Это очень плохо.
Но в нашем арсенале есть испытанное средство - каскадирование. Так, шестикаскадный CIC фильтр с подавлением алиасов не хуже -115 дБ нас уже вполне устроит (см. рис. ниже). За это мы должны заплатить ухудшившейся неравномерностью 0,9 дБ в целевой полосе, но это пустяки. При необходимости этот небольшой провал АЧХ можно потом скорректировать.
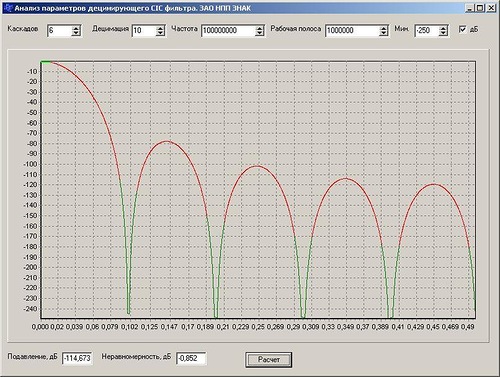
Конечно, сам по себе CIC фильтр не может обеспечить требуемую крутизну АЧХ для качественного выделения полосы целевого сигнала - это работа возлагается на FIR фильтр в следующем каскаде децимации.
Таким образом, для данного проекта наш дециматор получается двухкаскадным. В первом каскаде шестикаскадный CIC дециматор (который совсем без умножителей) берет всю грязную работу на себя и делит огромную скорость входного потока данных на 10, во втором каскаде FIR дециматор подчищает огрехи CIC, выполняет чистовую отделку и делит ещё на 4. Во втором каскаде уже требуется настоящий FIR фильтр с умножителями. Но он будет работать на пониженной в 10 раз частоте, и в ПЛИС его можно реализовать экономично, с работой умножителей в цикле - наподобие того, как это делается в программах для ЭВМ. Требования к АЧХ этого фильтра будут ниже, чем при однокаскадной децимации, и его порядок не будет высоким. Такой фильтр не отнимет у ПЛИС много ресурса. Часто для экономии умножителей применяют такую разновидность FIR фильтра, как полудиапазонный (half-band) фильтр с коэффициентом децимации 2 - у него половина коэффициентов равны нулю. Ну и, конечно, импульсная характеристика FIR фильтра должна быть обязательно симметричной - это не только дает нам линейную ФЧХ, но и в два раза экономит память в ПЛИС для их хранения.
Второй FIR каскад выгодно раздробить на подкаскады, например, из полудиапазонных фильтров. Это нам даст в целом ещё бОльшую экономию по умножителям.
Если общий коэффициент децимации DDC должен быть небольшим (менее 8-10, т.е. на выходе нам нужна широкая полоса), то CIC уже не подойдет, и надо будет раскошеливаться на FIR с умножителями, который также выгодно дробить на каскады.
Первые этапы ЦОС реализуются в большинстве современных широкополосных ЦРПУ аппаратно в ПЛИС FPGA, т.к. требуется очень высокая производительность. Но сегодня уже есть и альтернатива - алгоритмы ЦОС с достаточно высокой производительностью можно недорого распараллеливать и вычислять на GPU - видеокарте NVidia с поддержкой CUDA, СИ-подобного языка параллельных вычислений. Хватило бы скорости интерфейса закачать туда входной поток данных. Но в любом случае такая архитектура относится к классу SDR, т. к. определяется и настраивается программно при помощи прошивок ПЛИС или программного обеспечения GPU/CPU.
DDC можно реализовать и без использования ПЛИС и избежать связанных с этим граблей, временнЫх и материальных затрат освоения программных пакетов разработки прошивок FPGA. Промышленность супостатов выпускает готовые микросхемы DDC, которые можно извне программировать в рамках выполняющейся функции (программировать фильтры, настраивать коэффициенты децимации каскадов, перестраивать синтезатор и т. д.). В этом случае структура DDC ЦРПУ будет состоять из УРЧ, входного ФНЧ, АЦП, микросхемы DDC, контроллера и интерфейса с ЭВМ.
О подводных камнях.
1. Если ошибиться с выбором параметров децимирующих фильтров, то можно нарваться на внеполосные каналы приема, которые получаются из недостаточно подавленных алиасов.
2. Не надо забывать, что каждый каскад децимации должен сопровождаться расширением разрядности данных. Чем уже полоса, тем больше требуется разрядов для понижения шума округления (здесь действует принцип обмена разрядности на ширину полосы сигнала, см. подробнее в теме о выборе разрядности АЦП).
3. Не надо скупиться на разрядности умножителей в квадратурном преобразователе по входу LO опорного сигнала. И сам опорный сигнал, формируемый методом прямого цифрового синтеза DDS (Direct Digital Synthesizer), должен быть точным, насколько это возможно. Для повышения его точности часто применяют интерполяцию по-Тейлору, если в ПЛИС есть лишние умножители. Иногда недостаточно точный опорный сигнал искусственно зашумляют (dithering, дизеризация) для уменьшения спуров, при этом мощность спуров размазывается по частоте, незначительно повышая шумовой пьедестал. Чтобы сэкономить память ПЛИС и не хранить в ней таблицу значений функции косинуса, для вычисления этих значений иногда применяют итерационный алгоритм CORDIC.
Конечно, в таком коротком очерке нельзя рассмотреть все тонкости и нюансы реализации DDC и особенности аппаратной реализации ЦОС на ПЛИС. Но основной принцип и основные грабли должны быть понятны.
=========================================================
Литература. Гольденберг. Цифровая обработка сигналов
Ликбез про нерекурсивные (FIR, КИХ) и рекурсивные (IIR, БИХ) фильтры: http://www.dsplib.ru/content/filters/ch10/ch10.html
Про CIC фильтры: www.dsplib.ru/content/cic/cic.html
Рассмотрим типовую структуру КВ цифрового приемника с DDC дециматором.

Для конкретности пусть частота дискретизации АЦП будет 100 МГц, а ширина целевой полосы выходного сигнала 2 МГц. Берем "с потолка" запас 0,5 МГц на неидеальность децимирующего фильтра, итого получаем частоту дискретизации комплексного выходного сигнала 2,5 МГц. Таким образом, в процессе обработки требуется понизить (децимировать) частоту дискретизации в 40 раз. Вся обработка принятого сигнала (после АЦП) выполняется вычислительными алгоритмами цифровой обработки сигналов (ЦОС), то есть, достаточно точно.
На выходе АЦП мы имеем вещественный дискретный сигнал с симметричным относительно нуля периодическим спектром (период 100 МГц). Квадратурный преобразователь (DDS и два умножителя) формирует из этого вещественного сигнала комплексный дискретный сигнал и линейно сдвигает его спектр по оси частот так, чтобы центральная частота целевой полосы стала нулевой промежуточной частотой. При этом периодичность спектра сохраняется, но он перестает быть симметричным (это и понятно, сигнал стал комплексным), см. рисунок.

Цель дальнейшей фильтрации - из широкой 100-мегагерцовой полосы комплексного сигнала вырезать нужные нам 2 МГц в окрестности нулевой частоты с одновременным выполнением децимации. Эта операция выполняется параллельно в обоих I-Q каналах независимо друг от друга обычными дискретными (цифровыми) вещественными фильтрами. Фильтры должны быть абсолютно идентичными. Рекомендуется применять нерекурсивные фильтры с симметричными коэффициентами.
Операция децимации заключается в отбрасывании лишних отсчетов дискретного сигнала. Грубо говоря, на выходе из сорока пар исходных отсчетов сигнала должна остаться только одна пара. Так просто их отбросить нельзя, иначе будет эффект спектральных наложений (алайзинг), т.к. по сути децимация - это дискретизация дискретного сигнала. Т.е. перед отбрасыванием мы должны спектр сигнала привести к требованиям по-Котельникову, отфильтровать те частоты, которые превышают новую частоту Найквиста. От рекурсивных фильтров отказываемся, т.к. нам не нужна кривая ФЧХ. Значит, нерекурсивный FIR фильтр должен быть немалого порядка, с хорошим скатом АЧХ - ведь на расфильтровку у нас есть всего 500 кГц запаса.
Анализируя эту ситуацию, мы видим, что у нас нет такого огромного вычислительного ресурса - ведь оба децимирующих FIR фильтра должны работать на полной скорости 100 MSPS. Да и вообще - наша дешевая ПЛИС не имеет столько встроенных умножителей для их реализации. Что делать?
И тут нам на помощь приходит самая простейшая из всех простых форма реализации нерекурсивного фильтра - однородный фильтр. Это такой фильтр, все коэффициенты которого равны единице. То есть, он не требует умножителей совсем! Импульсная характеристика (взвешивающее окно) однородного фильтра - прямоугольная, а АЧХ (модуль преобразования Фурье импульсной характеристики) имеет многолепестковую форму, в которой лепестки образованы функцией вида |sinc x| = |sin x / x|. Затухание АЧХ в средних точках между лепестками бесконечное. Этот фильтр может быть реализован и в рекурсивном виде, так он получается еще проще. Теория однородного фильтра изложена у Гольденберга ("Цифровая обработка сигналов") на странице 77. Супостаты Гольденберга не читали, и рекурсивную реализацию однородного фильтра они по-своему обозвали CIC-фильтром (Cascaded Integral-Comb), или фильтром Хогенауэра.
К нашей радости оказывается, что его АЧХ как нельзя лучше подходит для реализации децимирующего фильтра, т.к. имеет глубокие провалы как раз на тех частотах, где требуется давить "алиасы". См. на рисунке АЧХ 1-каскадного CIC, рассчитанного для коэффициента децимации 10. Ось частот отградуирована в долях от исходной частоты дискретизации, т.е. 0,5 - это исходная частота Найквиста 50 МГц. Новая частота дискретизации после этого дециматора будет 100/10 = 10 МГц.

На картинке красным цветом показаны полосы частот, которые нас не интересуют вообще и где АЧХ может быть абсолютно любой (это и не целевая полоса и не алиасы), зеленым цветом близ нулевой частоты показана половина 2-мегагерцовой целевой полосы, также зеленым цветом вокруг провалов на частотах кратных новой частоте дискретизации 10 МГц (10, 20, 30, 40, 50 МГц) показаны 2-мегагерцовые участки "алиасов". К сожалению, эти провалы АЧХ не столь широки как нам хотелось бы, и на краях полезной полосы алиас первого порядка будет подавлен всего на 19 дБ. Это очень плохо.
Но в нашем арсенале есть испытанное средство - каскадирование. Так, шестикаскадный CIC фильтр с подавлением алиасов не хуже -115 дБ нас уже вполне устроит (см. рис. ниже). За это мы должны заплатить ухудшившейся неравномерностью 0,9 дБ в целевой полосе, но это пустяки. При необходимости этот небольшой провал АЧХ можно потом скорректировать.

Конечно, сам по себе CIC фильтр не может обеспечить требуемую крутизну АЧХ для качественного выделения полосы целевого сигнала - это работа возлагается на FIR фильтр в следующем каскаде децимации.
Таким образом, для данного проекта наш дециматор получается двухкаскадным. В первом каскаде шестикаскадный CIC дециматор (который совсем без умножителей) берет всю грязную работу на себя и делит огромную скорость входного потока данных на 10, во втором каскаде FIR дециматор подчищает огрехи CIC, выполняет чистовую отделку и делит ещё на 4. Во втором каскаде уже требуется настоящий FIR фильтр с умножителями. Но он будет работать на пониженной в 10 раз частоте, и в ПЛИС его можно реализовать экономично, с работой умножителей в цикле - наподобие того, как это делается в программах для ЭВМ. Требования к АЧХ этого фильтра будут ниже, чем при однокаскадной децимации, и его порядок не будет высоким. Такой фильтр не отнимет у ПЛИС много ресурса. Часто для экономии умножителей применяют такую разновидность FIR фильтра, как полудиапазонный (half-band) фильтр с коэффициентом децимации 2 - у него половина коэффициентов равны нулю. Ну и, конечно, импульсная характеристика FIR фильтра должна быть обязательно симметричной - это не только дает нам линейную ФЧХ, но и в два раза экономит память в ПЛИС для их хранения.
Второй FIR каскад выгодно раздробить на подкаскады, например, из полудиапазонных фильтров. Это нам даст в целом ещё бОльшую экономию по умножителям.
Если общий коэффициент децимации DDC должен быть небольшим (менее 8-10, т.е. на выходе нам нужна широкая полоса), то CIC уже не подойдет, и надо будет раскошеливаться на FIR с умножителями, который также выгодно дробить на каскады.
Первые этапы ЦОС реализуются в большинстве современных широкополосных ЦРПУ аппаратно в ПЛИС FPGA, т.к. требуется очень высокая производительность. Но сегодня уже есть и альтернатива - алгоритмы ЦОС с достаточно высокой производительностью можно недорого распараллеливать и вычислять на GPU - видеокарте NVidia с поддержкой CUDA, СИ-подобного языка параллельных вычислений. Хватило бы скорости интерфейса закачать туда входной поток данных. Но в любом случае такая архитектура относится к классу SDR, т. к. определяется и настраивается программно при помощи прошивок ПЛИС или программного обеспечения GPU/CPU.
DDC можно реализовать и без использования ПЛИС и избежать связанных с этим граблей, временнЫх и материальных затрат освоения программных пакетов разработки прошивок FPGA. Промышленность супостатов выпускает готовые микросхемы DDC, которые можно извне программировать в рамках выполняющейся функции (программировать фильтры, настраивать коэффициенты децимации каскадов, перестраивать синтезатор и т. д.). В этом случае структура DDC ЦРПУ будет состоять из УРЧ, входного ФНЧ, АЦП, микросхемы DDC, контроллера и интерфейса с ЭВМ.
О подводных камнях.
1. Если ошибиться с выбором параметров децимирующих фильтров, то можно нарваться на внеполосные каналы приема, которые получаются из недостаточно подавленных алиасов.
2. Не надо забывать, что каждый каскад децимации должен сопровождаться расширением разрядности данных. Чем уже полоса, тем больше требуется разрядов для понижения шума округления (здесь действует принцип обмена разрядности на ширину полосы сигнала, см. подробнее в теме о выборе разрядности АЦП).
3. Не надо скупиться на разрядности умножителей в квадратурном преобразователе по входу LO опорного сигнала. И сам опорный сигнал, формируемый методом прямого цифрового синтеза DDS (Direct Digital Synthesizer), должен быть точным, насколько это возможно. Для повышения его точности часто применяют интерполяцию по-Тейлору, если в ПЛИС есть лишние умножители. Иногда недостаточно точный опорный сигнал искусственно зашумляют (dithering, дизеризация) для уменьшения спуров, при этом мощность спуров размазывается по частоте, незначительно повышая шумовой пьедестал. Чтобы сэкономить память ПЛИС и не хранить в ней таблицу значений функции косинуса, для вычисления этих значений иногда применяют итерационный алгоритм CORDIC.
Конечно, в таком коротком очерке нельзя рассмотреть все тонкости и нюансы реализации DDC и особенности аппаратной реализации ЦОС на ПЛИС. Но основной принцип и основные грабли должны быть понятны.
=========================================================
Литература. Гольденберг. Цифровая обработка сигналов
Ликбез про нерекурсивные (FIR, КИХ) и рекурсивные (IIR, БИХ) фильтры: http://www.dsplib.ru/content/filters/ch10/ch10.html
Про CIC фильтры: www.dsplib.ru/content/cic/cic.html
Можно ли DDC реализовать при помощи вычислительно эффективной процедуры Быстрого Преобразования Фурье - FFT
Рассмотрим математическую модель дискретного преобразования Фурье некоторого дискретного вещественного сигнала x(k), которое вычисляется поблочно, с длиной блока N точек.
X(n) = <сумма k=0, N-1> [ x(k) exp (-i Wn k) ]
где
X(n) - комплексные дискретные значения спектра для текущего блока входного сигнала х(k) на кратных частотах Wn;
n - номер спектральной составляющей, n = 0, ... N-1;
k - дискретное время - номер отсчета исходного сигнала в блоке, k = 0, ... N-1;
N - количество точек в блоке сигнала, оно же равно количеству точек спектра на его периоде;
exp (-i Wn k) = cos (Wn k) - i sin (Wn k) - комплексная экспонента отрицательной частоты -Wn;
Wn = 2 пи n / N - это те дискретные нормированные частоты на интервале от 0 до двух пи радиан, для которых вычисляется спектр: W0 - нулевая частота постоянной составляющей, W1 - шаг по частоте, W(N/2) - частота Найквиста пи, WN - частота дискретизации 2 пи.
Не забываем, что спектр дискретного сигнала периодический, а период спектра N здесь равен нормированной частоте дискретизации 2 пи. Отсюда легко вычисляются все частоты Wn как в нормированном, так и в натуральном виде.
Что мы здесь видим? А видим то, что в этой модели есть много общего с DDC (т.е. это немного не доделанный DDC):
1. Умножение исходного вещественного сигнала х(k) на комплексную экспоненту некоторой отрицательной частоты -Wn. Такая операция в частотной области приводит к сдвигу двустороннего симметричного спектра исходного сигнала влево на величину Wn, после чего сигнал становится комплексным, а исходная частота Wn становится нулевой. Ровно эта же операция выполняется и в квадратурном преобразователе DDC.
2. Фильтрация сдвинутого по частоте сигнала однокаскадным CIC фильтром - однородным нерекурсивным фильтром нижних частот порядка N, с многолепестковой частотной характеристикой вида |sin x / x|. АЧХ этого фильтра см. на рисунке ниже. Этот фильтр в модели представлен операцией суммирования результатов умножения. Его импульсная характеристика задана неявно в виде прямоугольного единичного взвешивающего окна размером N точек, на которое умножается сигнал x(k) при формировании текущего блока данных. Операция фильтрации выполняется и в DDC, с тем лишь отличием, что там фильтр не является случайным, а специально проектируется для минимизации спектральных наложений при децимации, и CIC (да и то многокаскадный) применяется лишь в первых каскадах дециматора.
3. Децимация выходного сигнала в N раз. Действительно, для каждого частотного канала FFT (которые отличаются значениями Wn), на каждые N точек входного сигнала мы имеем только одно комплексное значение выходного сигнала X(n).
Итак, FFT можно рассматривать как N-канальную систему DDC, у которой частотные каналы по их центру настроены на частоты Wn. Каждый канал имеет выход в виде комплексной огибающей (complex envelope) на нулевой промежуточной частоте и с пониженной частотой дискретизации в N раз. Полоса и АЧХ каждого канала определяется фильтром по п. 2. С единственной лишь оговоркой - этот однокаскадный CIC фильтр дает неприемлемо большие спектральные наложения (алиасы) в каналах нашего DDC. Этой же причиной объясняется и такое явление, как "растекание спектра" (spectrum leakage) при FFT.
Можно ли побороть этот недостаток? Да, можно. Для этого нужно заменить прямоугольную взвешивающую (weighting) оконную функцию на такую, спектр которой обладал бы нужными нам свойствами. Подобных окон напридумано много разных (оконные функции Чебышева, Хэмминга, Ханна, Кайзера, Блэкмана и т.д. и.т.п.), для всех их характерно плавное спадание по краям во временной области и сильное подавление боковых лепестков спектра в частотной области. Иными словами, перед выполнением FFT каждый блок входного сигнала надо бы умножать на такого рода плавное взвешивающее окно. При этом АЧХ всех частотных каналов будут абсолютно идентичными и зависеть только от формы выбранной оконной функции (точнее, от модуля ее спектра).
Конечно же, никакие известные "оконные функции" в чистом виде нам не подходят, так как нам хотелось бы иметь ровную АЧХ в канале, а не "горбатую". Да ещё и с подавлением спектральных наложений не хуже сотни децибел. Значит, для нашего устройства придется проектировать своё собственное окно. Это дело несложное, и нужное нам окно (или что то же самое - импульсная характеристика фильтра, набор его коэффициентов) ищется при помощи обратного преобразования Фурье от требуемой комплексной частотной характеристики фильтра. Фильтр, не вносящий фазовых искажений, имеет симметричную импульсную характеристику (симметричное окно), а именно это нам и нужно. Окно хорошего качества при этом может достигать размера в несколько тысяч точек (шире окно - выше качество).
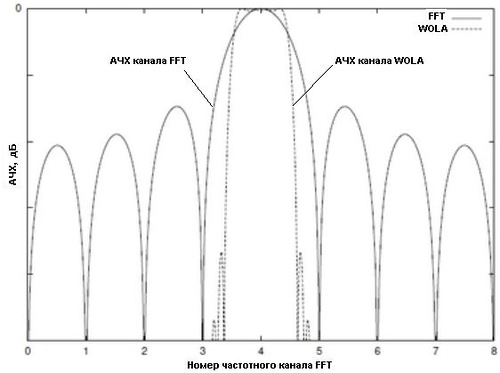
Часто требуется управлять коэффициентом перекрытия АЧХ смежных частотных каналов, отношением ширины окна к количеству частотных каналов, коэффициентом децимации и другими параметрами обработки. Поэтому для повышения гибкости этого алгоритма перед вычислением FFT применяют дополнительные операции: перекрытие блоков сигнала во времени до взвешивания (overlap) и полифазное суммирование его субблоков после взвешивания (add), не меняющие принципиальной сущности метода. Этот модифицированный алгоритм называется WOLA filterbank (Weighting, OverLap and Add) или по-русски - WOLA анализ, банк полифазных фильтров.
http://en.wikipedia.org/wiki/Filterbank
https://casper.berkeley.edu/wiki/The_Polyphase_Filter_Bank_Technique
http://www.dsplib.ru/content/polyphasefft/polyphase.html
Таким образом, при помощи вычислительно эффективного ядра N-точечного дискретного преобразования Фурье (Fast Fourier Transform), реализуется как бы "многоканальный DDC" в виде банка полосовых фильтров WOLA, в котором все N частотных каналов (а их могут быть сотни и тысячи), вычисляются совместно и одновременно. При этом фильтр, формирующий АЧХ всех каналов, является общим и вычисляется только один раз при взвешивании блока входного сигнала. Всё это в отличие от традиционного DDC, в котором каждый частотный канал вычисляется отдельно и должен иметь собственный децимирующий фильтр.
Недостатком такого банка полосовых фильтров является жестко фиксированный шаг каналов по частоте, а также их абсолютная идентичность по ширине полосы. Однако, при необходимости, несколько смежных частотных каналов на выходе банка можно объединить в один, более широкополосный канал. Эта несложная операция, обратная анализу, называется "синтез" и заключается в интерполяции (повышении частоты дискретизации), формирующей фильтрации объединяемых каналов, сдвиге их спектров на "свои места" и последующем суммировании. Цель формирующей фильтрации - обеспечить ровную АЧХ на стыках объединяемых каналов. Естественно, что все спектральные преобразования комплексных сигналов выполняются при помощи комплексного умножения на комплексную экспоненту cos wt +- i sin wt, при этом никакие побочные продукты и зеркальные каналы не образуются.
Поскольку выходные сигналы как DDC, так и банка полосовых фильтров являются комплексными, то так просто взять их и "послушать" не получится. Перед тем, как подать такой сигнал на воспроизведение, его нужно преобразовать к вещественному виду, то есть сделать спектр сигнала симметричным относительно нуля. А именно: выделить фильтром нужную полосу частот, преобразовать (сдвинуть) спектр в нужную нам сторону (например, для получения телеграфного тона или SSB сигнала) и затем просто отбросить, не вычисляя, мнимую часть результата преобразования. Естественное требование, что в результате фильтрации и сдвига спектра (перед отбрасыванием мнимой части), в нашем комплексном сигнале должны остаться только частоты одного знака (только положительные или только отрицательные). Иначе - "здравствуй, родной наш зеркальный канал", про который при цифровой обработке комплексных сигналов мы уже давно забыли.
Рассмотрим математическую модель дискретного преобразования Фурье некоторого дискретного вещественного сигнала x(k), которое вычисляется поблочно, с длиной блока N точек.
X(n) = <сумма k=0, N-1> [ x(k) exp (-i Wn k) ]
где
X(n) - комплексные дискретные значения спектра для текущего блока входного сигнала х(k) на кратных частотах Wn;
n - номер спектральной составляющей, n = 0, ... N-1;
k - дискретное время - номер отсчета исходного сигнала в блоке, k = 0, ... N-1;
N - количество точек в блоке сигнала, оно же равно количеству точек спектра на его периоде;
exp (-i Wn k) = cos (Wn k) - i sin (Wn k) - комплексная экспонента отрицательной частоты -Wn;
Wn = 2 пи n / N - это те дискретные нормированные частоты на интервале от 0 до двух пи радиан, для которых вычисляется спектр: W0 - нулевая частота постоянной составляющей, W1 - шаг по частоте, W(N/2) - частота Найквиста пи, WN - частота дискретизации 2 пи.
Не забываем, что спектр дискретного сигнала периодический, а период спектра N здесь равен нормированной частоте дискретизации 2 пи. Отсюда легко вычисляются все частоты Wn как в нормированном, так и в натуральном виде.
Что мы здесь видим? А видим то, что в этой модели есть много общего с DDC (т.е. это немного не доделанный DDC):
1. Умножение исходного вещественного сигнала х(k) на комплексную экспоненту некоторой отрицательной частоты -Wn. Такая операция в частотной области приводит к сдвигу двустороннего симметричного спектра исходного сигнала влево на величину Wn, после чего сигнал становится комплексным, а исходная частота Wn становится нулевой. Ровно эта же операция выполняется и в квадратурном преобразователе DDC.
2. Фильтрация сдвинутого по частоте сигнала однокаскадным CIC фильтром - однородным нерекурсивным фильтром нижних частот порядка N, с многолепестковой частотной характеристикой вида |sin x / x|. АЧХ этого фильтра см. на рисунке ниже. Этот фильтр в модели представлен операцией суммирования результатов умножения. Его импульсная характеристика задана неявно в виде прямоугольного единичного взвешивающего окна размером N точек, на которое умножается сигнал x(k) при формировании текущего блока данных. Операция фильтрации выполняется и в DDC, с тем лишь отличием, что там фильтр не является случайным, а специально проектируется для минимизации спектральных наложений при децимации, и CIC (да и то многокаскадный) применяется лишь в первых каскадах дециматора.
3. Децимация выходного сигнала в N раз. Действительно, для каждого частотного канала FFT (которые отличаются значениями Wn), на каждые N точек входного сигнала мы имеем только одно комплексное значение выходного сигнала X(n).
Итак, FFT можно рассматривать как N-канальную систему DDC, у которой частотные каналы по их центру настроены на частоты Wn. Каждый канал имеет выход в виде комплексной огибающей (complex envelope) на нулевой промежуточной частоте и с пониженной частотой дискретизации в N раз. Полоса и АЧХ каждого канала определяется фильтром по п. 2. С единственной лишь оговоркой - этот однокаскадный CIC фильтр дает неприемлемо большие спектральные наложения (алиасы) в каналах нашего DDC. Этой же причиной объясняется и такое явление, как "растекание спектра" (spectrum leakage) при FFT.
Можно ли побороть этот недостаток? Да, можно. Для этого нужно заменить прямоугольную взвешивающую (weighting) оконную функцию на такую, спектр которой обладал бы нужными нам свойствами. Подобных окон напридумано много разных (оконные функции Чебышева, Хэмминга, Ханна, Кайзера, Блэкмана и т.д. и.т.п.), для всех их характерно плавное спадание по краям во временной области и сильное подавление боковых лепестков спектра в частотной области. Иными словами, перед выполнением FFT каждый блок входного сигнала надо бы умножать на такого рода плавное взвешивающее окно. При этом АЧХ всех частотных каналов будут абсолютно идентичными и зависеть только от формы выбранной оконной функции (точнее, от модуля ее спектра).
Конечно же, никакие известные "оконные функции" в чистом виде нам не подходят, так как нам хотелось бы иметь ровную АЧХ в канале, а не "горбатую". Да ещё и с подавлением спектральных наложений не хуже сотни децибел. Значит, для нашего устройства придется проектировать своё собственное окно. Это дело несложное, и нужное нам окно (или что то же самое - импульсная характеристика фильтра, набор его коэффициентов) ищется при помощи обратного преобразования Фурье от требуемой комплексной частотной характеристики фильтра. Фильтр, не вносящий фазовых искажений, имеет симметричную импульсную характеристику (симметричное окно), а именно это нам и нужно. Окно хорошего качества при этом может достигать размера в несколько тысяч точек (шире окно - выше качество).

Часто требуется управлять коэффициентом перекрытия АЧХ смежных частотных каналов, отношением ширины окна к количеству частотных каналов, коэффициентом децимации и другими параметрами обработки. Поэтому для повышения гибкости этого алгоритма перед вычислением FFT применяют дополнительные операции: перекрытие блоков сигнала во времени до взвешивания (overlap) и полифазное суммирование его субблоков после взвешивания (add), не меняющие принципиальной сущности метода. Этот модифицированный алгоритм называется WOLA filterbank (Weighting, OverLap and Add) или по-русски - WOLA анализ, банк полифазных фильтров.
http://en.wikipedia.org/wiki/Filterbank
https://casper.berkeley.edu/wiki/The_Polyphase_Filter_Bank_Technique
http://www.dsplib.ru/content/polyphasefft/polyphase.html
Таким образом, при помощи вычислительно эффективного ядра N-точечного дискретного преобразования Фурье (Fast Fourier Transform), реализуется как бы "многоканальный DDC" в виде банка полосовых фильтров WOLA, в котором все N частотных каналов (а их могут быть сотни и тысячи), вычисляются совместно и одновременно. При этом фильтр, формирующий АЧХ всех каналов, является общим и вычисляется только один раз при взвешивании блока входного сигнала. Всё это в отличие от традиционного DDC, в котором каждый частотный канал вычисляется отдельно и должен иметь собственный децимирующий фильтр.
Недостатком такого банка полосовых фильтров является жестко фиксированный шаг каналов по частоте, а также их абсолютная идентичность по ширине полосы. Однако, при необходимости, несколько смежных частотных каналов на выходе банка можно объединить в один, более широкополосный канал. Эта несложная операция, обратная анализу, называется "синтез" и заключается в интерполяции (повышении частоты дискретизации), формирующей фильтрации объединяемых каналов, сдвиге их спектров на "свои места" и последующем суммировании. Цель формирующей фильтрации - обеспечить ровную АЧХ на стыках объединяемых каналов. Естественно, что все спектральные преобразования комплексных сигналов выполняются при помощи комплексного умножения на комплексную экспоненту cos wt +- i sin wt, при этом никакие побочные продукты и зеркальные каналы не образуются.
Поскольку выходные сигналы как DDC, так и банка полосовых фильтров являются комплексными, то так просто взять их и "послушать" не получится. Перед тем, как подать такой сигнал на воспроизведение, его нужно преобразовать к вещественному виду, то есть сделать спектр сигнала симметричным относительно нуля. А именно: выделить фильтром нужную полосу частот, преобразовать (сдвинуть) спектр в нужную нам сторону (например, для получения телеграфного тона или SSB сигнала) и затем просто отбросить, не вычисляя, мнимую часть результата преобразования. Естественное требование, что в результате фильтрации и сдвига спектра (перед отбрасыванием мнимой части), в нашем комплексном сигнале должны остаться только частоты одного знака (только положительные или только отрицательные). Иначе - "здравствуй, родной наш зеркальный канал", про который при цифровой обработке комплексных сигналов мы уже давно забыли.
О разрядности АЦП
Рассмотрим один парадоксальный вопрос из области цифровой обработки сигналов, по которому неспециалисты часто впадают в заблуждение.
Какую разрядность должен иметь АЦП, чтобы реализовать некоторую цифровую систему с некоторой заданной рабочей полосой частот целевого полезного сигнала? Неважно - будет ли это автомагнитола, эквалайзер или SDR приемник.
Ответ - разрядность АЦП может быть любой, начиная с 1 бита. Кажется, тут какой-то парадокс. А как же ошибка квантования, шум квантования - ведь при малой разрядности шум квантования просто обязан быть гигантским! А вот и нет.
Всё в мире относительно.
При выборе разрядности АЦП нужно соотнести ширину полосы Найквиста дискретного сигнала после АЦП (в DDC-SDR это где-то 50 МГц) с шириной полосы целевого полезного сигнала (в магнитоле это 20 кГц, а в КВ приемнике - всего 3 кГц и даже меньше). И чем это отношение выше, тем больше мы сможем сэкономить на разрядах АЦП.
Существенным в этой авантюре является то, что в процессе поэтапной обработки высокоскоростного и низкоразрядного сигнала с АЦП, с переходом на каждом этапе к более узкой полосе и более низкой частоте дискретизации (эта операция называется децимацией), мы не должны забывать о соответствующем повышении разрядности данных при их цифровой фильтрации перед выполнением непосредственно прореживания данных.
Этот прием широко применяется в технике. Примеры - так называемые сигма-дельта АЦП с умопомрачительно высокой разрядностью выходного кода или широко рекламированные несколько лет назад так называемые однобитовые автомагнитолы. Это всё из одной оперы. Все эти приборы работают на очень высокой частоте дискретизации - в десятки и сотни раз превышающие требования теоремы Котельникова. Достоинством таких однобитовых систем является исключительно высокая линейность, как это ни парадоксально звучит для принципиально нелинейного устройства - однобитового порогового квантователя.
Можно ещё один пример привести - всем известная ШИМ - широтно-импульсная модуляция. Это не что иное, как однобитовая система ЦАП / АЦП.
Можно подойти к объяснению этого феномена и с другой стороны - с привлечением аппарата мат. статистики. Как известно, шум квантования имеет равномерный закон распределения, а его мощность (дисперсия) зависит только от шага квантования. Повышаем шаг квантования (понижая разрядность) - в квадратичной зависимости будет возрастать и мощность шума. Тут, конечно, пока всё верно.
Но не надо забывать, что в частотной области мощность шума квантования равномерно распределена по всей полосе Найквиста. И чем шире эта полоса по отношению к нашей полезной целевой полосе, тем меньшая доля мощности шума квантования попадёт в эту нашу полезную полосу. И тем выше будет итоговое отношение сигнал-шум. Как видите, всё просто.
В этом и заключается принцип обмена разрядности АЦП на частоту дискретизации, позволяющий гибко подходить к выбору аппаратной части. Если мы хотим сэкономить на одном параметре, то должны повысить требования к другому. И наоборот.
Рассмотрим один парадоксальный вопрос из области цифровой обработки сигналов, по которому неспециалисты часто впадают в заблуждение.
Какую разрядность должен иметь АЦП, чтобы реализовать некоторую цифровую систему с некоторой заданной рабочей полосой частот целевого полезного сигнала? Неважно - будет ли это автомагнитола, эквалайзер или SDR приемник.
Ответ - разрядность АЦП может быть любой, начиная с 1 бита. Кажется, тут какой-то парадокс. А как же ошибка квантования, шум квантования - ведь при малой разрядности шум квантования просто обязан быть гигантским! А вот и нет.
Всё в мире относительно.
При выборе разрядности АЦП нужно соотнести ширину полосы Найквиста дискретного сигнала после АЦП (в DDC-SDR это где-то 50 МГц) с шириной полосы целевого полезного сигнала (в магнитоле это 20 кГц, а в КВ приемнике - всего 3 кГц и даже меньше). И чем это отношение выше, тем больше мы сможем сэкономить на разрядах АЦП.
Существенным в этой авантюре является то, что в процессе поэтапной обработки высокоскоростного и низкоразрядного сигнала с АЦП, с переходом на каждом этапе к более узкой полосе и более низкой частоте дискретизации (эта операция называется децимацией), мы не должны забывать о соответствующем повышении разрядности данных при их цифровой фильтрации перед выполнением непосредственно прореживания данных.
Этот прием широко применяется в технике. Примеры - так называемые сигма-дельта АЦП с умопомрачительно высокой разрядностью выходного кода или широко рекламированные несколько лет назад так называемые однобитовые автомагнитолы. Это всё из одной оперы. Все эти приборы работают на очень высокой частоте дискретизации - в десятки и сотни раз превышающие требования теоремы Котельникова. Достоинством таких однобитовых систем является исключительно высокая линейность, как это ни парадоксально звучит для принципиально нелинейного устройства - однобитового порогового квантователя.
Можно ещё один пример привести - всем известная ШИМ - широтно-импульсная модуляция. Это не что иное, как однобитовая система ЦАП / АЦП.
Можно подойти к объяснению этого феномена и с другой стороны - с привлечением аппарата мат. статистики. Как известно, шум квантования имеет равномерный закон распределения, а его мощность (дисперсия) зависит только от шага квантования. Повышаем шаг квантования (понижая разрядность) - в квадратичной зависимости будет возрастать и мощность шума. Тут, конечно, пока всё верно.
Но не надо забывать, что в частотной области мощность шума квантования равномерно распределена по всей полосе Найквиста. И чем шире эта полоса по отношению к нашей полезной целевой полосе, тем меньшая доля мощности шума квантования попадёт в эту нашу полезную полосу. И тем выше будет итоговое отношение сигнал-шум. Как видите, всё просто.
В этом и заключается принцип обмена разрядности АЦП на частоту дискретизации, позволяющий гибко подходить к выбору аппаратной части. Если мы хотим сэкономить на одном параметре, то должны повысить требования к другому. И наоборот.
О работе приемника DDC и передатчика DUC в высших зонах Найквиста
Из теории дискретных сигналов известно, что:
1. Спектр дискретного сигнала периодически повторяется на бесконечном интервале частот с периодом, равным частоте дискретизации Fs. Половина периода спектра называется зоной Найквиста (см. рис.). Спектры в четных и нечетных зонах взаимно инверсны.
2. При дискретизации и восстановлении вещественного видеосигнала (спектр которого ограничен только сверху) частота дискретизации Fs по-Котельникову должна быть больше удвоенной ширины спектра этого сигнала. Если сигнал комплексный, то требования к Fs смягчаются в два раза. Спектр видеосигнала должен целиком находиться в первой зоне Найквиста. Восстановление выполняется фильтром нижних частот, полоса пропускания которого целиком должна находиться также в первой зоне Найквиста.
3. При дискретизации и восстановлении вещественного радиосигнала (спектр которого ограничен и снизу и сверху) частота дискретизации Fs также должна быть больше удвоенной ширины спектра этого сигнала. Спектр радиосигнала должен целиком находиться в любой выбранной зоне Найквиста. Восстановление выполняется полосовым фильтром, полоса пропускания которого также должна целиком находиться в любой (возможно, что и другой) зоне Найквиста.
Этот случай (п. 3) называется субдискретизацией, при этом частота дискретизации не удовлетворяет условию Котельникова для видеосигнала, а может быть во много раз ниже. Применяя только операции дискретизации и восстановления, можно из видеосигнала получить радиосигнал и наоборот, а также гонять радиосигнал между разными зонами Найквиста. Это свойство дискретных сигналов позволяет нам использовать цифровой DDC КВ приемник для приема УКВ радиосигналов. А также непосредственно формировать УКВ радиосигнал в DUC КВ передатчике.
Во временнОй области математической моделью операции дискретизации в АЦП является линейная свёртка (http://www.dsplib.ru/content/conv/conv.html) исходного непрерывного сигнала S(t), взятого в дискретные моменты времени kTs, и дискретизирующего импульса So(t):
Sд(t) = <сумма k=-oo, +oo> [ S(kTs) So(t-kTs) ],
где Sд(t) - дискретный сигнал, t - непрерывное время, Ts - интервал дискретизации, k - номер дискретного отсчета, <Сумма>[] - операция суммирования в указанных пределах индекса k, oo - обозначение символа бесконечности.
В частотной области в левой части модели мы имеем спектр дискретного сигнала, а в правой части - нашей свёртке соответствует произведение спектра исходного сигнала, взятого в дискретные моменты времени, и спектра дискретизирующего импульса. Это утверждение следует из свойства преобразования Фурье о взаимной трансформации свёртки в произведение.
Всё это в теории. А эта теория (в части п.1 о бесконечной и незатухающей периодичности спектра) верна только для идеального случая, когда в качестве дискретизирующего импульса So(t) принята дельта-функция - импульс прямоугольной формы бесконечно малой длительности и единичной площади. Так как спектр дельта-функции есть единичная константа на всех частотах, то на спектр дискретного сигнала идеальный дискретизирующий импульс никак не влияет.
В реальных АЦП и ЦАП дискретизирующий импульс далек от идеала, т. к. имеет конечную ненулевую длительность (To) и форму, отличную от прямоугольной. Это приводит к искажениям АЧХ преобразователей ЦАП/АЦП, потере энергии сигнала в высших зонах Найквиста, ухудшению отношения сигнал-шум приемника.
Иллюстрация механизма влияния этой неидеальности приведена на рисунке. Если дискретизирующий импульс имеет прямоугольную форму, то его амплитудный спектр есть многолепестковая функция вида |sin x / x|, ширина лепестков которой обратно пропорциональна длительности импульса.
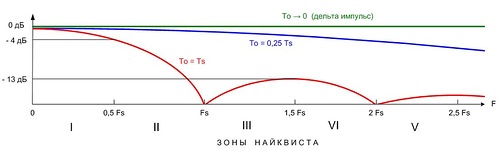
На рисунке приведены нормированные спектры дискретизирующего прямоугольного импульса для трех случаев:
- идеальный дискретизирующий импульс дельта-функция (зеленый);
- неидеальный импульс с длительностью в четверть интервала дискретизации To = Ts / 4 (синий);
- наихудший случай, когда длительность дискретизирующего импульса равна интервалу дискретизации To = Ts (красный). Этот случай характерен для ЦАП со ступенчатым выходным сигналом и для интегрирующих АЦП.
Мы видим, что в наилучшем случае идеальный дискретизирующий импульс имеет постоянный единичный спектр (зеленый график с бесконечно широким главным лепестком спектра), и его умножение на спектр исходного сигнала не приведет ни к малейшим искажениям АЧХ.
В наихудшем случае (красный график с узкими лепестками спектра) даже при работе только в первой зоне Найквиста мы будем иметь подавление сигнала на частоте Найквиста 4 дБ. О работе в других зонах Найквиста здесь и речи быть не может, т.к. в них затухание сигнала может быть очень большим или даже бесконечным.
Уменьшение длительности дискретизирующего импульса приводит к расширению его спектра и улучшению ситуации. Например, если его укоротить в 4 раза (синий график с расширенными в 4 раза лепестками спектра), то уже вполне сносно можно работать в первых трех-четырех зонах Найквиста. К слову, АЦП LTC2208 имеет дискретизирующий импульс To = Ts / 2, что делает весьма проблематичной его работу в зонах Найквиста выше третьей, где затухание сигнала будет превышать 9 дБ.
Выводы. Для работы в высших зонах Найквиста:
1. Следует выбирать АЦП с малой длительностью дискретизирующего импульса (АЦП с малой апертурой). В этом смысле качество АЦП определяет та его аналоговая часть, которая называется устройством выборки и хранения (УВХ, sample and hold circuit), выборка сигнала в котором должна выполняться очень быстро, в течение малой доли интервала дискретизации.
2. ЦАП должен формировать на выходе (перед полосовым фильтром) не ступенчатый дискретный сигнал, как это обычно происходит, а сигнал в виде коротких прямоугольных импульсов.
Из теории дискретных сигналов известно, что:
1. Спектр дискретного сигнала периодически повторяется на бесконечном интервале частот с периодом, равным частоте дискретизации Fs. Половина периода спектра называется зоной Найквиста (см. рис.). Спектры в четных и нечетных зонах взаимно инверсны.
2. При дискретизации и восстановлении вещественного видеосигнала (спектр которого ограничен только сверху) частота дискретизации Fs по-Котельникову должна быть больше удвоенной ширины спектра этого сигнала. Если сигнал комплексный, то требования к Fs смягчаются в два раза. Спектр видеосигнала должен целиком находиться в первой зоне Найквиста. Восстановление выполняется фильтром нижних частот, полоса пропускания которого целиком должна находиться также в первой зоне Найквиста.
3. При дискретизации и восстановлении вещественного радиосигнала (спектр которого ограничен и снизу и сверху) частота дискретизации Fs также должна быть больше удвоенной ширины спектра этого сигнала. Спектр радиосигнала должен целиком находиться в любой выбранной зоне Найквиста. Восстановление выполняется полосовым фильтром, полоса пропускания которого также должна целиком находиться в любой (возможно, что и другой) зоне Найквиста.
Этот случай (п. 3) называется субдискретизацией, при этом частота дискретизации не удовлетворяет условию Котельникова для видеосигнала, а может быть во много раз ниже. Применяя только операции дискретизации и восстановления, можно из видеосигнала получить радиосигнал и наоборот, а также гонять радиосигнал между разными зонами Найквиста. Это свойство дискретных сигналов позволяет нам использовать цифровой DDC КВ приемник для приема УКВ радиосигналов. А также непосредственно формировать УКВ радиосигнал в DUC КВ передатчике.
Во временнОй области математической моделью операции дискретизации в АЦП является линейная свёртка (http://www.dsplib.ru/content/conv/conv.html) исходного непрерывного сигнала S(t), взятого в дискретные моменты времени kTs, и дискретизирующего импульса So(t):
Sд(t) = <сумма k=-oo, +oo> [ S(kTs) So(t-kTs) ],
где Sд(t) - дискретный сигнал, t - непрерывное время, Ts - интервал дискретизации, k - номер дискретного отсчета, <Сумма>[] - операция суммирования в указанных пределах индекса k, oo - обозначение символа бесконечности.
В частотной области в левой части модели мы имеем спектр дискретного сигнала, а в правой части - нашей свёртке соответствует произведение спектра исходного сигнала, взятого в дискретные моменты времени, и спектра дискретизирующего импульса. Это утверждение следует из свойства преобразования Фурье о взаимной трансформации свёртки в произведение.
Всё это в теории. А эта теория (в части п.1 о бесконечной и незатухающей периодичности спектра) верна только для идеального случая, когда в качестве дискретизирующего импульса So(t) принята дельта-функция - импульс прямоугольной формы бесконечно малой длительности и единичной площади. Так как спектр дельта-функции есть единичная константа на всех частотах, то на спектр дискретного сигнала идеальный дискретизирующий импульс никак не влияет.
В реальных АЦП и ЦАП дискретизирующий импульс далек от идеала, т. к. имеет конечную ненулевую длительность (To) и форму, отличную от прямоугольной. Это приводит к искажениям АЧХ преобразователей ЦАП/АЦП, потере энергии сигнала в высших зонах Найквиста, ухудшению отношения сигнал-шум приемника.
Иллюстрация механизма влияния этой неидеальности приведена на рисунке. Если дискретизирующий импульс имеет прямоугольную форму, то его амплитудный спектр есть многолепестковая функция вида |sin x / x|, ширина лепестков которой обратно пропорциональна длительности импульса.

На рисунке приведены нормированные спектры дискретизирующего прямоугольного импульса для трех случаев:
- идеальный дискретизирующий импульс дельта-функция (зеленый);
- неидеальный импульс с длительностью в четверть интервала дискретизации To = Ts / 4 (синий);
- наихудший случай, когда длительность дискретизирующего импульса равна интервалу дискретизации To = Ts (красный). Этот случай характерен для ЦАП со ступенчатым выходным сигналом и для интегрирующих АЦП.
Мы видим, что в наилучшем случае идеальный дискретизирующий импульс имеет постоянный единичный спектр (зеленый график с бесконечно широким главным лепестком спектра), и его умножение на спектр исходного сигнала не приведет ни к малейшим искажениям АЧХ.
В наихудшем случае (красный график с узкими лепестками спектра) даже при работе только в первой зоне Найквиста мы будем иметь подавление сигнала на частоте Найквиста 4 дБ. О работе в других зонах Найквиста здесь и речи быть не может, т.к. в них затухание сигнала может быть очень большим или даже бесконечным.
Уменьшение длительности дискретизирующего импульса приводит к расширению его спектра и улучшению ситуации. Например, если его укоротить в 4 раза (синий график с расширенными в 4 раза лепестками спектра), то уже вполне сносно можно работать в первых трех-четырех зонах Найквиста. К слову, АЦП LTC2208 имеет дискретизирующий импульс To = Ts / 2, что делает весьма проблематичной его работу в зонах Найквиста выше третьей, где затухание сигнала будет превышать 9 дБ.
Выводы. Для работы в высших зонах Найквиста:
1. Следует выбирать АЦП с малой длительностью дискретизирующего импульса (АЦП с малой апертурой). В этом смысле качество АЦП определяет та его аналоговая часть, которая называется устройством выборки и хранения (УВХ, sample and hold circuit), выборка сигнала в котором должна выполняться очень быстро, в течение малой доли интервала дискретизации.
2. ЦАП должен формировать на выходе (перед полосовым фильтром) не ступенчатый дискретный сигнал, как это обычно происходит, а сигнал в виде коротких прямоугольных импульсов.
Зачем нужна рандомизация выходного кода АЦП в приемнике DDC-SDR
Некоторые высококачественные и высокодинамичные АЦП (к примеру, тот же LTC2208 и др.) имеют режим работы с рандомизацией выходного кода. В этом режиме выходной код АЦП, передаваемый по внешней параллельной шине данных, делается случайным. Рандомизация выполняется очень просто - все разряды выходного кода, кроме младшего, суммируются по модулю 2 со значением младшего разряда. И поскольку младший разряд всегда шумит, выходной код АЦП также становится случайным. Естественно, то устройство, которое принимает этот код (например, ПЛИС), должно выполнить обратную операцию для его восстановления.
Зачем это нужно? А нужно это затем, чтобы в некоторой степени нивелировать последствия плохой развязки аналоговых и цифровых цепей АЦП из-за неудачной разводки печатной платы.
Один из сильных источников влияния цифровых цепей на чувствительный аналоговый вход АЦП - это выходные буферы данных самого АЦП, которые при переключении потребляют по шинам питания значительный импульсный ток. Если на вход АЦП подать синусоиду или любой другой периодический сигнал, то разряды выходного кода станут "хлопать" так же периодически, причём каждый разряд - со своим периодом. В результате этого, из-за плохой развязки, на вход АЦП наводится периодическая помеха. Спектр помехи имеет множество дискретных спектральных составляющих (шпор, spurs), которые возвышаются над шумовым пьедесталом.
Рандомизация нужна для того, чтобы убрать периодичность переключения разрядов выходного кода и сделать их случайными. При этом наводка никуда не девается, но она перестает быть периодичной, и мощность шпор ровным тонким слоем размазывается по спектру в частотной области. Естественно, это приводит к небольшому повышению шумового пьедестала и соответствующему ухудшению чувствительности приемника.
Хороший способ проверить правильность разводки АЦП - это включить и выключить режим рандомизации. Если при включении рандомизации пьедестал шума поднялся - значит есть проблема с развязкой цепей, но это также значит, что есть и резерв для дальнейшего повышения чувствительности и динамического диапазона приемника. Если разводка выполнена правильно, режим рандомизации включать не требуется.
Некоторые высококачественные и высокодинамичные АЦП (к примеру, тот же LTC2208 и др.) имеют режим работы с рандомизацией выходного кода. В этом режиме выходной код АЦП, передаваемый по внешней параллельной шине данных, делается случайным. Рандомизация выполняется очень просто - все разряды выходного кода, кроме младшего, суммируются по модулю 2 со значением младшего разряда. И поскольку младший разряд всегда шумит, выходной код АЦП также становится случайным. Естественно, то устройство, которое принимает этот код (например, ПЛИС), должно выполнить обратную операцию для его восстановления.
Зачем это нужно? А нужно это затем, чтобы в некоторой степени нивелировать последствия плохой развязки аналоговых и цифровых цепей АЦП из-за неудачной разводки печатной платы.
Один из сильных источников влияния цифровых цепей на чувствительный аналоговый вход АЦП - это выходные буферы данных самого АЦП, которые при переключении потребляют по шинам питания значительный импульсный ток. Если на вход АЦП подать синусоиду или любой другой периодический сигнал, то разряды выходного кода станут "хлопать" так же периодически, причём каждый разряд - со своим периодом. В результате этого, из-за плохой развязки, на вход АЦП наводится периодическая помеха. Спектр помехи имеет множество дискретных спектральных составляющих (шпор, spurs), которые возвышаются над шумовым пьедесталом.
Рандомизация нужна для того, чтобы убрать периодичность переключения разрядов выходного кода и сделать их случайными. При этом наводка никуда не девается, но она перестает быть периодичной, и мощность шпор ровным тонким слоем размазывается по спектру в частотной области. Естественно, это приводит к небольшому повышению шумового пьедестала и соответствующему ухудшению чувствительности приемника.
Хороший способ проверить правильность разводки АЦП - это включить и выключить режим рандомизации. Если при включении рандомизации пьедестал шума поднялся - значит есть проблема с развязкой цепей, но это также значит, что есть и резерв для дальнейшего повышения чувствительности и динамического диапазона приемника. Если разводка выполнена правильно, режим рандомизации включать не требуется.
Нужна ли дизеризация в DDC-SDR приемнике
В предыдущем сообщении мы рассмотрели благотворное влияние искусственного зашумления на характеристики АЦП. Дизеризация - это тоже искусственное зашумление, но уже не сигнала помехи, а полезного входного сигнала АЦП. Некоторые высококачественные АЦП (например, LTC2208) имеют режим работы с встроенной дизеризацией.
Ранее мы уже рассматривали применение дизеризации в цифровом синтезаторе частоты DDS для декорреляции ошибки квантования выходного сигнала синтезатора. Зачем же дизеризация нужна в АЦП? Ведь на первый взгляд зашумление полезного сигнала может только всё ухудшить. На самом деле резон есть.
Если рассматривать ошибку округления результата преобразования входного сигнала в АЦП (шум квантования), то не всегда этот шум является белым (то есть с равномерной спектральной плотностью) и относительно безвредным. Очень часто шум квантования сильно коррелирован (взаимосвязан) с входным сигналом. Например, если на вход АЦП мы подали одну единственную синусоиду, то шум квантования будет иметь явно выраженную периодичность, от чего на спектре появятся опять те же самые шпоры. Метод избавления от шпор нам уже известен - нужно декоррелировать шум квантования. Это достигается зашумлением одного-двух младших значащих бит выходного кода АЦП, благодаря чему мощность шпор равномерно размазывается по частоте. Обычно шум добавляется на входе АЦП в аналоговом виде, но могут быть и другие варианты. Можно добавлять как белый, так и "окрашенный" шум - его спектральные характеристики большого значения не имеют, лишь бы он был достаточно широкополосен. Окрашенный шум добавляют тогда, когда есть возможность вынести его спектр за пределы рабочей полосы частот входных сигналов.
Этот прием применяется в случаях, когда при эксплуатации устройств допустимо наличие на входе одного или нескольких периодических сигналов, а собственные шумы устройства малы. Например, в измерительных приборах, спектроанализаторах, профессиональной звуковой аппаратуре.
В цифровом приемнике применять дизеризацию не требуется, если, конечно, этот приемник использовать по назначению, а не в качестве измерительного прибора. Но дизеризация окрашенным шумом нужна при измерении технических параметров цифрового приемника, когда эфирного шума нет, а испытательные сигналы подаются от генератора. При этом спектр вносимого шума выносят за пределы рабочего диапазона частот приемника.
Как только мы подключим к приемнику антенну, никакого дополнительного зашумления входного сигнала уже не потребуется. Широкополосный сигнал с антенны - лучший на свете дизеризатор.
В предыдущем сообщении мы рассмотрели благотворное влияние искусственного зашумления на характеристики АЦП. Дизеризация - это тоже искусственное зашумление, но уже не сигнала помехи, а полезного входного сигнала АЦП. Некоторые высококачественные АЦП (например, LTC2208) имеют режим работы с встроенной дизеризацией.
Ранее мы уже рассматривали применение дизеризации в цифровом синтезаторе частоты DDS для декорреляции ошибки квантования выходного сигнала синтезатора. Зачем же дизеризация нужна в АЦП? Ведь на первый взгляд зашумление полезного сигнала может только всё ухудшить. На самом деле резон есть.
Если рассматривать ошибку округления результата преобразования входного сигнала в АЦП (шум квантования), то не всегда этот шум является белым (то есть с равномерной спектральной плотностью) и относительно безвредным. Очень часто шум квантования сильно коррелирован (взаимосвязан) с входным сигналом. Например, если на вход АЦП мы подали одну единственную синусоиду, то шум квантования будет иметь явно выраженную периодичность, от чего на спектре появятся опять те же самые шпоры. Метод избавления от шпор нам уже известен - нужно декоррелировать шум квантования. Это достигается зашумлением одного-двух младших значащих бит выходного кода АЦП, благодаря чему мощность шпор равномерно размазывается по частоте. Обычно шум добавляется на входе АЦП в аналоговом виде, но могут быть и другие варианты. Можно добавлять как белый, так и "окрашенный" шум - его спектральные характеристики большого значения не имеют, лишь бы он был достаточно широкополосен. Окрашенный шум добавляют тогда, когда есть возможность вынести его спектр за пределы рабочей полосы частот входных сигналов.
Этот прием применяется в случаях, когда при эксплуатации устройств допустимо наличие на входе одного или нескольких периодических сигналов, а собственные шумы устройства малы. Например, в измерительных приборах, спектроанализаторах, профессиональной звуковой аппаратуре.
В цифровом приемнике применять дизеризацию не требуется, если, конечно, этот приемник использовать по назначению, а не в качестве измерительного прибора. Но дизеризация окрашенным шумом нужна при измерении технических параметров цифрового приемника, когда эфирного шума нет, а испытательные сигналы подаются от генератора. При этом спектр вносимого шума выносят за пределы рабочего диапазона частот приемника.
Как только мы подключим к приемнику антенну, никакого дополнительного зашумления входного сигнала уже не потребуется. Широкополосный сигнал с антенны - лучший на свете дизеризатор.
Об инверсии спектра дискретного (цифрового) сигнала
На практике часто возникает потребность проинвертировать спектр дискретного сигнала. Например, преобразовать сигнал USB в LSB. Или устранить нежелательные последствия спектральной инверсии после операций преобразования спектра или дискретизации в четных зонах Найквиста.
С учетом того, что спектр дискретного сигнала является периодическим, то для инверсии спектра вещественного сигнала нужно его сдвинуть вправо или влево (без разницы) на величину сдвига, равную частоте Найквиста FN. Для этого наш сигнал надо умножить на комплексную экспоненту с частотой Найквиста. При этом спектральная составляющая нулевой частоты переходит на частоту Найквиста и наоборот. А спектр в целом инвертируется относительно центральных частот каждой зоны Найквиста.
В реальности это очень простая операция. Исходную вещественную последовательность требуется умножить на периодическую последовательность 1, -1, 1, -1, ..., то есть просто сменить знак каждого второго отсчета. Значения этой последовательности суть дискретные отсчеты косинусоиды, частота которой равна половине частоты дискретизации Fs, т.е. равна частоте Найквиста. При этом соответствующие значения синусоиды равны нулю, а значит мнимую часть вычислять не нужно. В результате получаем такой же вещественный сигнал, как и исходный, но с инверсным спектром.
Для того, чтобы проинвертировать спектр комплексного сигнала относительно нулевой частоты, нужно действительную и мнимую части сигнала поменять местами. При этом положительные частоты станут отрицательными, а отрицательные - положительными.
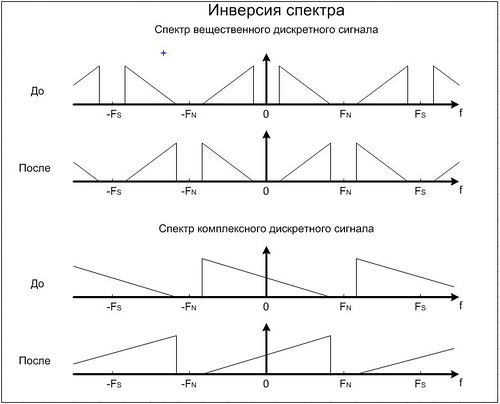
http://r4n.su/forum/viewtopic.php?f=28&t=331&p=2199#p2176
На практике часто возникает потребность проинвертировать спектр дискретного сигнала. Например, преобразовать сигнал USB в LSB. Или устранить нежелательные последствия спектральной инверсии после операций преобразования спектра или дискретизации в четных зонах Найквиста.
С учетом того, что спектр дискретного сигнала является периодическим, то для инверсии спектра вещественного сигнала нужно его сдвинуть вправо или влево (без разницы) на величину сдвига, равную частоте Найквиста FN. Для этого наш сигнал надо умножить на комплексную экспоненту с частотой Найквиста. При этом спектральная составляющая нулевой частоты переходит на частоту Найквиста и наоборот. А спектр в целом инвертируется относительно центральных частот каждой зоны Найквиста.
В реальности это очень простая операция. Исходную вещественную последовательность требуется умножить на периодическую последовательность 1, -1, 1, -1, ..., то есть просто сменить знак каждого второго отсчета. Значения этой последовательности суть дискретные отсчеты косинусоиды, частота которой равна половине частоты дискретизации Fs, т.е. равна частоте Найквиста. При этом соответствующие значения синусоиды равны нулю, а значит мнимую часть вычислять не нужно. В результате получаем такой же вещественный сигнал, как и исходный, но с инверсным спектром.
Для того, чтобы проинвертировать спектр комплексного сигнала относительно нулевой частоты, нужно действительную и мнимую части сигнала поменять местами. При этом положительные частоты станут отрицательными, а отрицательные - положительными.

http://r4n.su/forum/viewtopic.php?f=28&t=331&p=2199#p2176